Location

2012/05/22 00:00:33 42.686 23.009 9.4 5.60 Bulgaria

Arrival Times (from USGS)

Felt Map

Focal Mechanism

USGS/SLU Moment Tensor Solution ENS 2012/05/22 00:00:33:1 42.69 23.01 9.4 5.6 Bulgaria Stations used: CZ.JAVC CZ.KRUC HT.CHOS HU.BUD KO.GADA KO.KULA MN.AQU MN.DIVS MN.IDI OE.ARSA OE.CONA OE.MOA OE.MYKA OE.OBKA RO.BMR RO.BZS RO.CFR RO.DEV RO.HUMR RO.LOT SL.BOJS SL.CADS SL.CEY SL.CRES SL.CRNS SL.DOBS SL.GBAS SL.GBRS SL.GCIS SL.GORS SL.GROS SL.JAVS SL.KNDS SL.KOGS SL.LJU SL.MOZS Filtering commands used: hp c 0.01 n 3 lp c 0.03 n 3 Best Fitting Double Couple Mo = 2.16e+24 dyne-cm Mw = 5.49 Z = 12 km Plane Strike Dip Rake NP1 109 60 -93 NP2 295 30 -85 Principal Axes: Axis Value Plunge Azimuth T 2.16e+24 15 201 N 0.00e+00 2 111 P -2.16e+24 75 11 Moment Tensor: (dyne-cm) Component Value Mxx 1.60e+24 Mxy 6.54e+23 Mxz -1.05e+24 Myy 2.61e+23 Myz -3.07e+23 Mzz -1.87e+24 ############## ###################### ############################ ###-----------------########## ##------------------------######## #----------------------------####### --------------------------------###### #----------------------------------##### #------------------ --------------#### ####---------------- P ---------------#### #####--------------- ----------------### #######--------------------------------### ##########------------------------------## ############---------------------------# ################-----------------------# #####################--------------### #################################### ################################## ####### #################### ###### T ################### ### ################ ############## Global CMT Convention Moment Tensor: R T P -1.87e+24 -1.05e+24 3.07e+23 -1.05e+24 1.60e+24 -6.54e+23 3.07e+23 -6.54e+23 2.61e+23 Details of the solution is found at http://www.eas.slu.edu/eqc/eqc_mt/MECH.NA/20120522000033/index.html

Preferred Solution

The preferred solution from an analysis of the surface-wave spectral amplitude radiation pattern, waveform inversion and first motion observations is

      STK = 295
      DIP = 30
     RAKE = -85
       MW = 5.49
       HS = 12.0

The waveform inversion is preferred.

Moment Tensor Comparison

The following compares this source inversion to others

SLU USGSMT GCMT

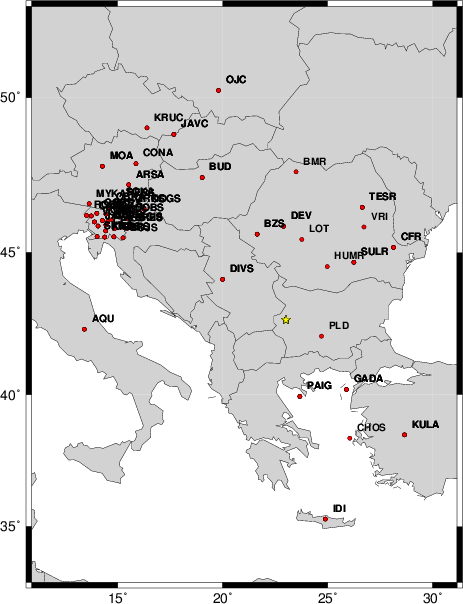
USGS/SLU Moment Tensor Solution ENS 16228041/-116325328:16322548:01:0 16325328:16322548:01:0 0.00 0.00 0.0 0.0 Stations used: CZ.JAVC CZ.KRUC HT.CHOS HU.BUD KO.GADA KO.KULA MN.AQU MN.DIVS MN.IDI OE.ARSA OE.CONA OE.MOA OE.MYKA OE.OBKA RO.BMR RO.BZS RO.CFR RO.DEV RO.DRGR RO.HUMR RO.LOT RO.MLR SL.BOJS SL.CADS SL.CEY SL.CRES SL.CRNS SL.DOBS SL.GBAS SL.GBRS SL.GCIS SL.GORS SL.GROS SL.JAVS SL.KNDS SL.KOGS SL.LJU SL.MOZS Filtering commands used: hp c 0.01 n 3 lp c 0.03 n 3 Best Fitting Double Couple Mo = 2.16e+24 dyne-cm Mw = 5.49 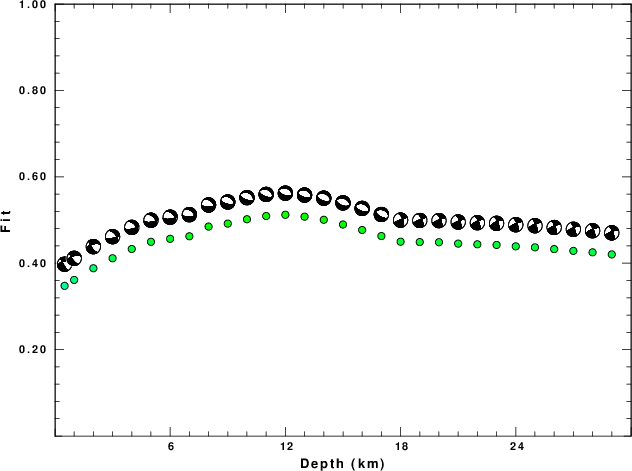Z = 12 km 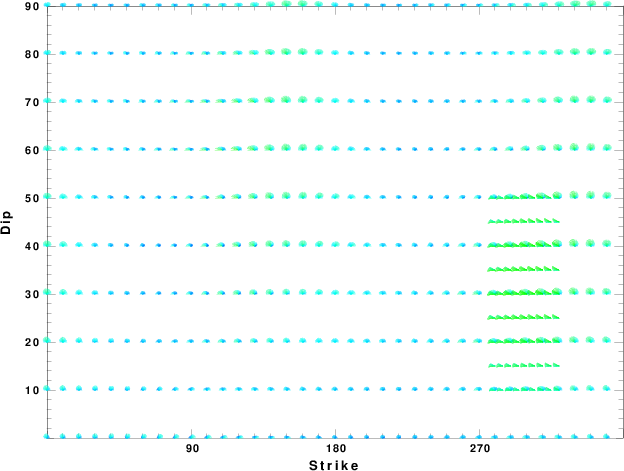Plane Strike Dip Rake NP1 108 61 -96 NP2 300 30 -80 Principal Axes: Axis Value Plunge Azimuth T 2.16e+24 15 203 N 0.00e+00 5 111 P -2.16e+24 74 4 Moment Tensor: (dyne-cm) Component Value Mxx 1.55e+24 Mxy 7.05e+23 Mxz -1.08e+24 Myy 2.99e+23 Myz -2.51e+23 Mzz -1.84e+24 ############## ###################### ########----################ ##------------------########## #------------------------######### -----------------------------####### --------------------------------###### ------------------- ------------###### #------------------ P --------------#### ####---------------- ---------------#### #####---------------------------------#### #######--------------------------------### ##########-----------------------------### ############--------------------------## ################-----------------------# #####################-------------###- #################################### ################################## ####### #################### ###### T ################### ### ################ ############## Global CMT Convention Moment Tensor: R T P -1.84e+24 -1.08e+24 2.51e+23 -1.08e+24 1.55e+24 -7.05e+23 2.51e+23 -7.05e+23 2.99e+23 USGS/SLU Moment Tensor Solution ENS 2012/05/22 00:00:33:1 42.69 23.01 9.4 5.6 Bulgaria Stations used: CZ.JAVC CZ.KRUC HT.CHOS HU.BUD KO.GADA KO.KULA MN.AQU MN.DIVS MN.IDI OE.ARSA OE.CONA OE.MOA OE.MYKA OE.OBKA RO.BMR RO.BZS RO.CFR RO.DEV RO.HUMR RO.LOT SL.BOJS SL.CADS SL.CEY SL.CRES SL.CRNS SL.DOBS SL.GBAS SL.GBRS SL.GCIS SL.GORS SL.GROS SL.JAVS SL.KNDS SL.KOGS SL.LJU SL.MOZS Filtering commands used: hp c 0.01 n 3 lp c 0.03 n 3 Best Fitting Double Couple Mo = 2.16e+24 dyne-cm Mw = 5.49 Z = 12 km Plane Strike Dip Rake NP1 109 60 -93 NP2 295 30 -85 Principal Axes: Axis Value Plunge Azimuth T 2.16e+24 15 201 N 0.00e+00 2 111 P -2.16e+24 75 11 Moment Tensor: (dyne-cm) Component Value Mxx 1.60e+24 Mxy 6.54e+23 Mxz -1.05e+24 Myy 2.61e+23 Myz -3.07e+23 Mzz -1.87e+24 ############## ###################### ############################ ###-----------------########## ##------------------------######## #----------------------------####### --------------------------------###### #----------------------------------##### #------------------ --------------#### ####---------------- P ---------------#### #####--------------- ----------------### #######--------------------------------### ##########------------------------------## ############---------------------------# ################-----------------------# #####################--------------### #################################### ################################## ####### #################### ###### T ################### ### ################ ############## Global CMT Convention Moment Tensor: R T P -1.87e+24 -1.05e+24 3.07e+23 -1.05e+24 1.60e+24 -6.54e+23 3.07e+23 -6.54e+23 2.61e+23 Details of the solution is found at http://www.eas.slu.edu/eqc/eqc_mt/MECH.NA/20120522000033/index.html

USGS Body-Wave Moment Tensor
USGS Body-Wave Moment Tensor Solution BULGARIA 12/05/22 00:00:33.11 Epicenter: 42.686 23.009 MW 5.6 USGS MOMENT TENSOR SOLUTION Depth 9 No. of sta: 49 Moment Tensor; Scale 10**17 Nm Mrr=-2.54 Mtt= 1.33 Mpp= 1.21 Mrt=-0.52 Mrp=-0.06 Mtp=-1.80 Principal axes: T Val= 3.09 Plg= 3 Azm=224 N -0.46 11 133 P -2.64 79 331 Best Double Couple:Mo=2.9*10**17 NP1:Strike=124 Dip=49 Slip=-104 NP2: 325 43 -74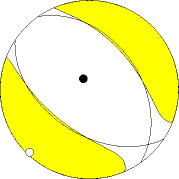
USGS WPhase Moment Tensor
USGS WPhase Moment Solution BULGARIA 12/05/22 0:00:33 Epicenter: 42.682 23.017 MW 5.6 USGS/WPHASE CENTROID MOMENT TENSOR 12/05/22 00:00:33.00 Centroid: 42.482 23.153 Depth 25 No. of sta: 26 Moment Tensor; Scale 10**17 Nm Mrr=-2.81 Mtt= 1.91 Mpp= 0.90 Mrt=-1.06 Mrp= 0.87 Mtp=-1.27 Principal axes: T Val= 3.08 Plg=13 Azm=214 N = 0.04 1 305 P = -3.12 76 43 Best Double Couple:Mo=3.1*10**17 NP1:Strike=302 Dip=32 Slip= -93 NP2: 126 58 -87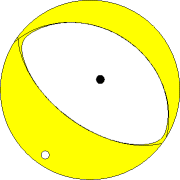

May 22, 2012, BULGARIA, MW=5.6 Howard Koss Meredith Nettles CENTROID-MOMENT-TENSOR SOLUTION GCMT EVENT: C201205220000A DATA: II LD IU DK CU G GE MN IC L.P.BODY WAVES:108S, 179C, T= 40 MANTLE WAVES: 60S, 63C, T=125 SURFACE WAVES: 128S, 266C, T= 50 TIMESTAMP: Q-20120522054611 CENTROID LOCATION: ORIGIN TIME: 00:00:36.6 0.1 LAT:42.55N 0.01;LON: 23.02E 0.01 DEP: 12.0 FIX;TRIANG HDUR: 1.6 MOMENT TENSOR: SCALE 10**24 D-CM RR=-2.890 0.028; TT= 2.130 0.028 PP= 0.762 0.027; RT=-1.770 0.081 RP= 0.415 0.088; TP=-1.650 0.023 PRINCIPAL AXES: 1.(T) VAL= 3.680;PLG=15;AZM=211 2.(N) -0.224; 10; 119 3.(P) -3.454; 72; 355 BEST DBLE.COUPLE:M0= 3.57*10**24 NP1: STRIKE=316;DIP=32;SLIP= -70 NP2: STRIKE=113;DIP=61;SLIP=-102 ########### ################### --------------######### -------------------######## ----------------------####### -------------------------###### #------------- ---------##### ###------------ P ----------##### #####---------- -----------#### #######----------------------#### #########---------------------### ###########------------------## ################-------------## ###########################-- ##### ##################- ### T ################# # ############### ###########

Waveform Inversion

The focal mechanism was determined using broadband seismic waveforms. The location of the event and the and stations used for the waveform inversion are shown in the next figure.

Location of broadband stations used for waveform inversion

The program wvfgrd96 was used with good traces observed at short distance to determine the focal mechanism, depth and seismic moment. This technique requires a high quality signal and well determined velocity model for the Green functions. To the extent that these are the quality data, this type of mechanism should be preferred over the radiation pattern technique which requires the separate step of defining the pressure and tension quadrants and the correct strike.

The observed and predicted traces are filtered using the following gsac commands:

hp c 0.01 n 3
lp c 0.03 n 3

The results of this grid search from 0.5 to 19 km depth are as follow:

           DEPTH  STK   DIP  RAKE   MW    FIT
WVFGRD96    0.5   150    75   -40   5.22 0.3477
WVFGRD96    1.0   145    65   -35   5.22 0.3613
WVFGRD96    2.0   145    65   -35   5.26 0.3884
WVFGRD96    3.0   325    45   -30   5.33 0.4115
WVFGRD96    4.0   320    40   -35   5.37 0.4330
WVFGRD96    5.0   320    40   -40   5.39 0.4495
WVFGRD96    6.0   320    40   -40   5.39 0.4566
WVFGRD96    7.0   315    40   -50   5.41 0.4624
WVFGRD96    8.0   315    35   -50   5.45 0.4849
WVFGRD96    9.0   305    30   -70   5.49 0.4918
WVFGRD96   10.0   300    30   -80   5.50 0.5018
WVFGRD96   11.0   300    30   -80   5.50 0.5093
WVFGRD96   12.0   295    30   -85   5.49 0.5122
WVFGRD96   13.0   295    30   -85   5.49 0.5078
WVFGRD96   14.0   295    35   -85   5.48 0.5006
WVFGRD96   15.0   110    55   -90   5.47 0.4897
WVFGRD96   16.0   110    55   -90   5.46 0.4769
WVFGRD96   17.0   120    60   -80   5.46 0.4629
WVFGRD96   18.0   340    60     5   5.40 0.4498
WVFGRD96   19.0   340    60    10   5.40 0.4490
WVFGRD96   20.0   340    65    10   5.41 0.4487
WVFGRD96   21.0   340    65    10   5.41 0.4454
WVFGRD96   22.0   340    70    20   5.42 0.4438
WVFGRD96   23.0   340    70    20   5.42 0.4424
WVFGRD96   24.0   340    70    15   5.43 0.4391
WVFGRD96   25.0   340    75    20   5.43 0.4368
WVFGRD96   26.0   340    75    20   5.44 0.4327
WVFGRD96   27.0   340    75    20   5.44 0.4286
WVFGRD96   28.0   340    75    20   5.44 0.4252
WVFGRD96   29.0   340    75    15   5.45 0.4204

The best solution is

WVFGRD96   12.0   295    30   -85   5.49 0.5122

The mechanism correspond to the best fit is

Figure 1. Waveform inversion focal mechanism

The best fit as a function of depth is given in the following figure:

Figure 2. Depth sensitivity for waveform mechanism

The comparison of the observed and predicted waveforms is given in the next figure. The red traces are the observed and the blue are the predicted. Each observed-predicted component is plotted to the same scale and peak amplitudes are indicated by the numbers to the left of each trace. A pair of numbers is given in black at the right of each predicted traces. The upper number it the time shift required for maximum correlation between the observed and predicted traces. This time shift is required because the synthetics are not computed at exactly the same distance as the observed and because the velocity model used in the predictions may not be perfect. A positive time shift indicates that the prediction is too fast and should be delayed to match the observed trace (shift to the right in this figure). A negative value indicates that the prediction is too slow. The lower number gives the percentage of variance reduction to characterize the individual goodness of fit (100% indicates a perfect fit).

The bandpass filter used in the processing and for the display was

hp c 0.01 n 3
lp c 0.03 n 3

Figure 3. Waveform comparison for selected depth

Focal mechanism sensitivity at the preferred depth. The red color indicates a very good fit to thewavefroms. Each solution is plotted as a vector at a given value of strike and dip with the angle of the vector representing the rake angle, measured, with respect to the upward vertical (N) in the figure.

A check on the assumed source location is possible by looking at the time shifts between the observed and predicted traces. The time shifts for waveform matching arise for several reasons:

The origin time and epicentral distance are incorrect
The velocity model used for the inversion is incorrect
The velocity model used to define the P-arrival time is not the same as the velocity model used for the waveform inversion (assuming that the initial trace alignment is based on the P arrival time)

Assuming only a mislocation, the time shifts are fit to a functional form:

 Time_shift = A + B cos Azimuth + C Sin Azimuth

The time shifts for this inversion lead to the next figure:

The derived shift in origin time and epicentral coordinates are given at the bottom of the figure.

Discussion

Acknowledgements

Thanks also to the many seismic network operators whose dedication make this effort possible: University of Nevada Reno, University of Alaska, University of Washington, Oregon State University, University of Utah, Montana Bureas of Mines, UC Berkely, Caltech, UC San Diego, Saint Louis University, University of Memphis, Lamont Doherty Earth Observatory, the Iris stations and the Transportable Array of EarthScope.

Velocity Model

The WUS model used for the waveform synthetic seismograms and for the surface wave eigenfunctions and dispersion is as follows:

MODEL.01
Model after     8 iterations
ISOTROPIC
KGS
FLAT EARTH
1-D
CONSTANT VELOCITY
LINE08
LINE09
LINE10
LINE11
      H(KM)   VP(KM/S)   VS(KM/S) RHO(GM/CC)         QP         QS       ETAP       ETAS      FREFP      FREFS
     1.9000     3.4065     2.0089     2.2150  0.302E-02  0.679E-02   0.00       0.00       1.00       1.00    
     6.1000     5.5445     3.2953     2.6089  0.349E-02  0.784E-02   0.00       0.00       1.00       1.00    
    13.0000     6.2708     3.7396     2.7812  0.212E-02  0.476E-02   0.00       0.00       1.00       1.00    
    19.0000     6.4075     3.7680     2.8223  0.111E-02  0.249E-02   0.00       0.00       1.00       1.00    
     0.0000     7.9000     4.6200     3.2760  0.164E-10  0.370E-10   0.00       0.00       1.00       1.00

Quality Control

Here we tabulate the reasons for not using certain digital data sets

BUR01 RO  - amplitudes are too large - gain problem?
LOT   RO  - R and T not used. The R is well fit but the T has Rayleigh on it
MLR   RO  - amplitudes are too large by about a factor of 4 or so
DRGR  RO  - amplitude are too large by about a factor of 4 or so
BMR   RO  - Z and R not used since noisy
KULA  RO  - amplitude are soo large by about a factor of 2
CUC   MN  - not used since path across Adriatic
AQU   MN -  Z R not used because of Adriatic path - Good shape to Love
            wave but need slowere model

The following stations did not have a valid response files:

Last Changed Wed May 23 03:04:59 CDT 2012