This tutorial shows how to use the Computer Programs in
Seismology codes to compute the static deformation for a given
finite fault model.
The solution for static deformation in a wholespace, halfspace
and a layer isotropic media are given in the file static.pdf.
Two program are used: hsanal96 and hstat96. The
first is used for the special problem of an observation point
anywhere within an isotropic halfspace or at the surface of an
isotropic halfspace. The program is an implementation of the
close-form solutions given in the PDF document. The second
program, hstat96, is much more general and will permit a
source and observation point anywhere within a stack of isotropic
layers with boundary conditions of halfspace, free or rigid at the
top and bottom interfaces. hstat96 is essentially the
limiting case of hspec96 as angular frequency goes to
zero. Because of its generality, the execution time of hstat96
is greater because of the multiplication of propagator matrices and
the numerical integration over wavenumber.
The sequence of running these two programs is as simple as
running hspec96:
which is the sequence same sequence as for running hspec96. There are two differences though. First the hspec96 creates the output file hspec96.grn which is then convolved with the source time function to create the ASCII file in the file96 format, e.g.,hprep96 -M ${MODEL} -d dfile -ALL -HS ${EVDP} -HR 0 -TF -BH
hsanal96
hprep96 -M ${MODEL} -d dfile -ALL -HS ${EVDP} -HR 0 -TF -BH
hstat96
Since the static deformation is just a single point, the hstat96 and hsanal96 directly create an output named file96. The other difference is that both programs accept a -V command line flag. The interesting part of the output is the following:hpulse96 -p -V -l 1 > file96
| hsanal96 |
hstat96 |
TSTATIC: 1 ZDD 1 -1.41254714E-06 |
HSTATIC: 1 ZDD 1 -1.41254611E-06 |
Unpack the DOSTATIC.tgz using the commands:
gunzip -c DOSTATIC.tgz | tar xvf -
This will create the following directory structure:
STATIC_TEST-|
|-FINITE_1
|
|-FINITE_2
|
|-FINITE_3
|
|-FINITE_4
In each sub-directory there will be an executable shell script named
DOIT. This shell script computes the static deformation of a finite
fault model and then plots a contour map.
The individual test cases differ in the following way:
These cases test the code and also investigate the sensitivity of the permanent displacements to the velocity model used.
Each of the directories that are unpacked contain a script named
DOIT. Follow the link to an annotated discussion of
the script DOIT.
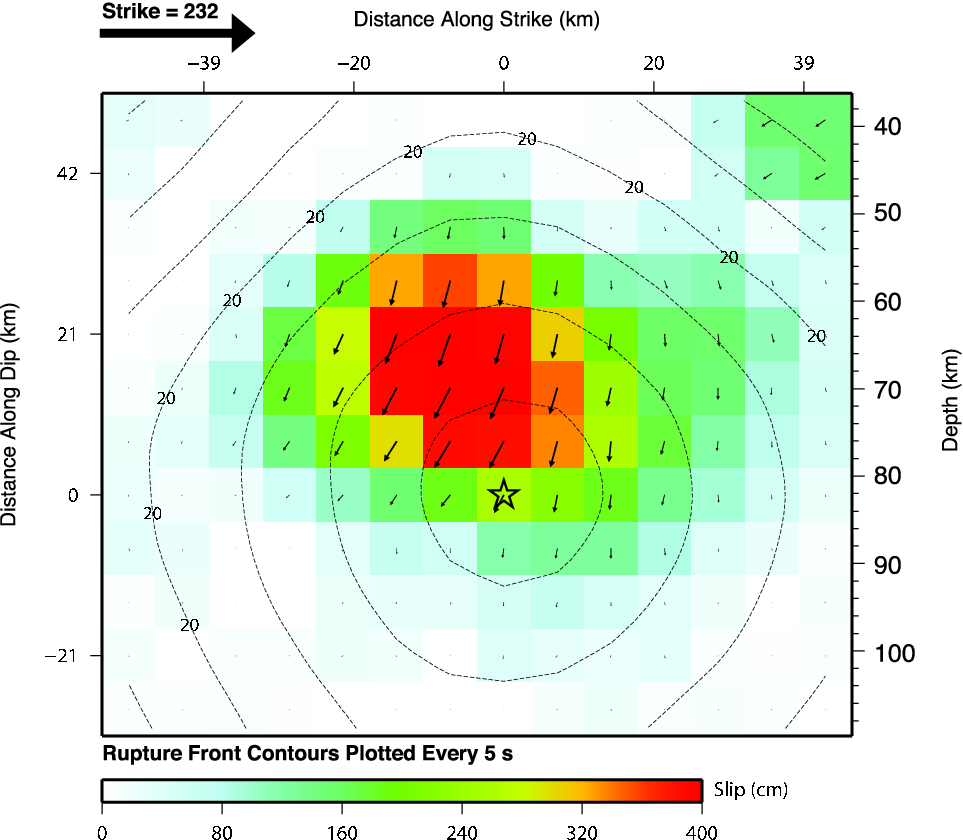
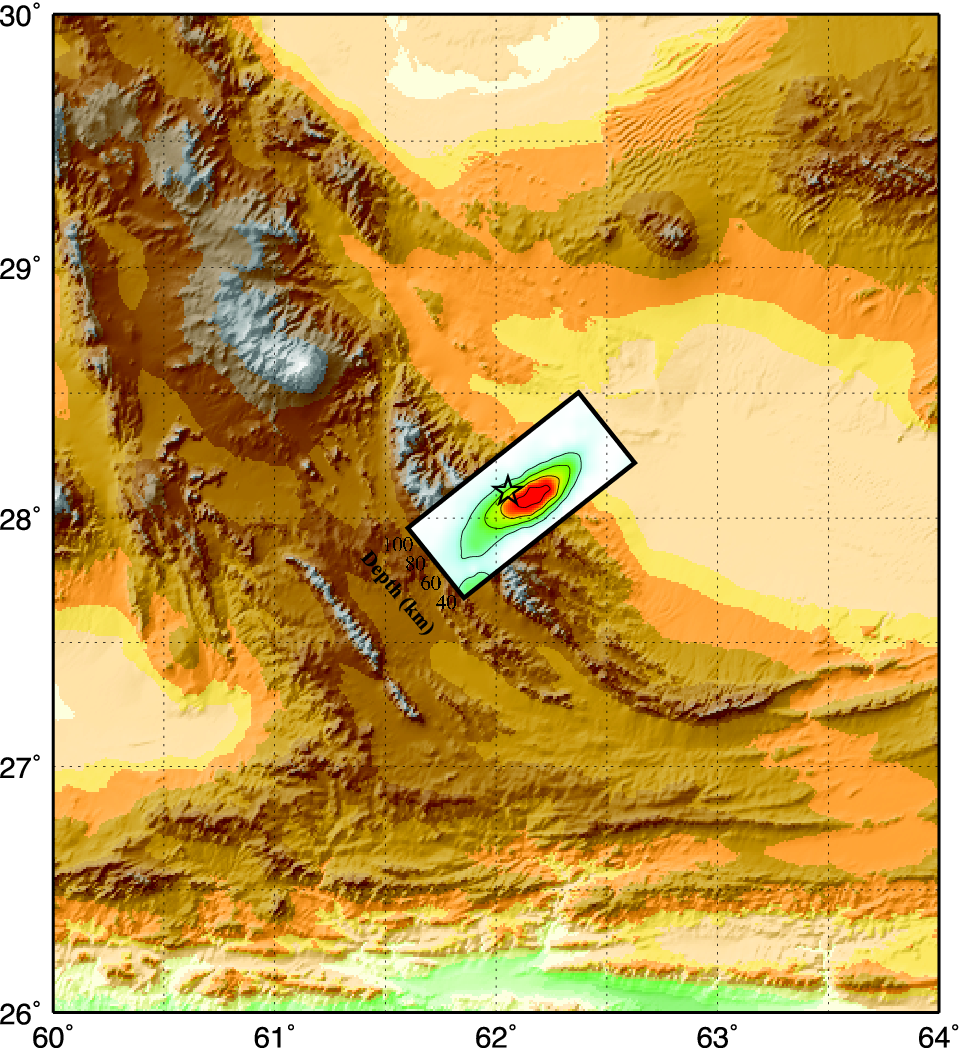
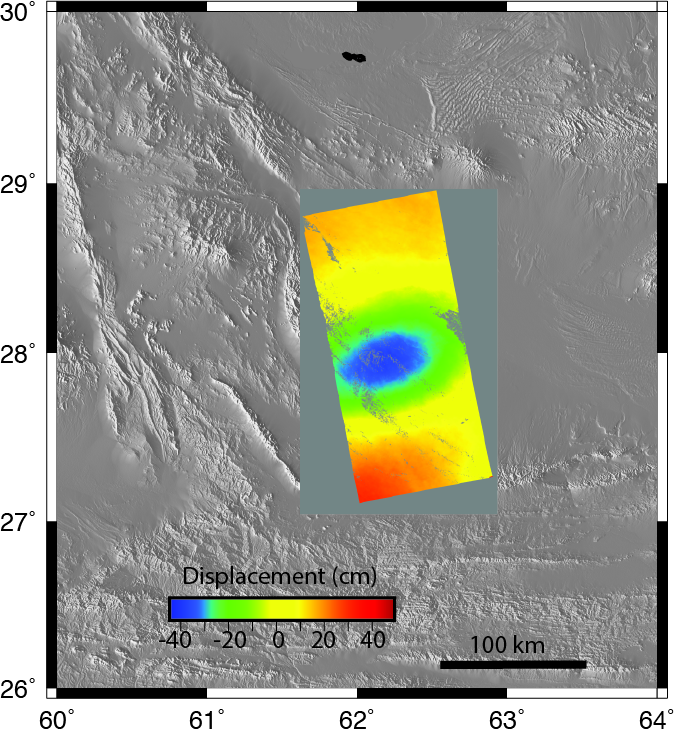
The example uses the finite fault solution for the M7.7
- 83km E of Khash, Iran (2013-04-16 10:44:20 UTC) earthquake.
We use the "Subfault Format" as the data file for the simulation.
The following three figures present the finite fault solution
(left) and the projection of the slip distribution onto topography
(center) and INSAR image (right).
 |
 |
 |
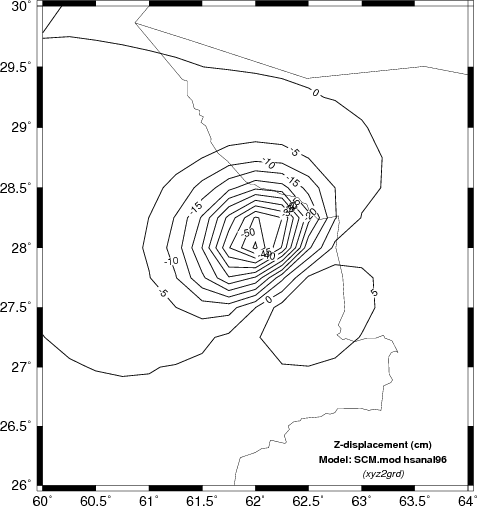
The first test is whether the hstat96 give the same
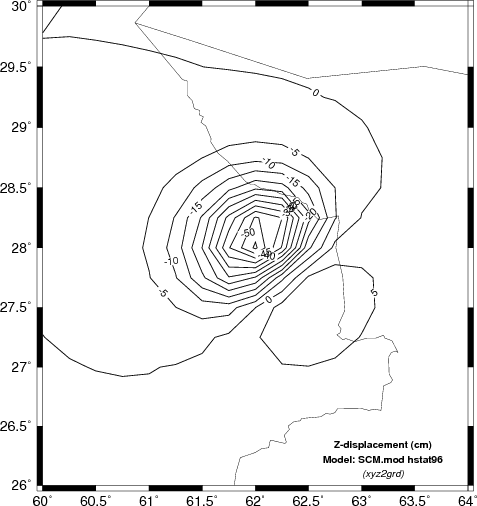
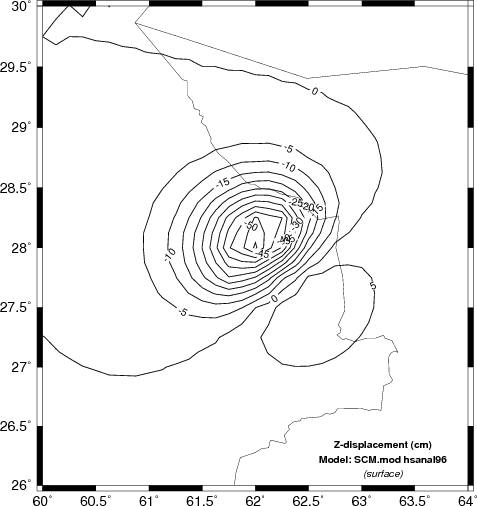
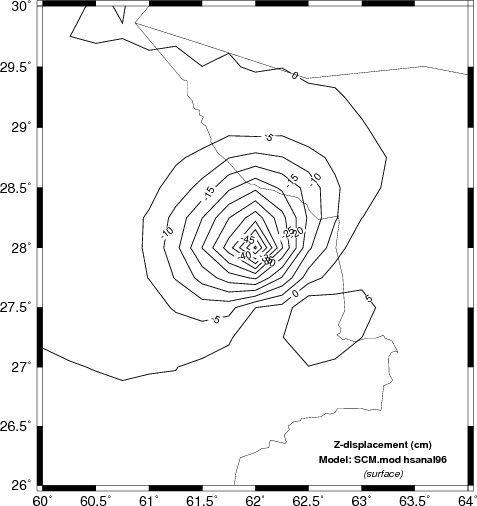
results as hsanal96 for a halfspace. Only the Z component
predictions are compared. We will compare the results of using the
GMT commands surface and xyz2grd. The shell script
uses a finer sampling for surface.
Vertical deformation (cm) for the halfspace model. The left shows the result of using the analytic solution hsanal96 while |
|
 |
 |
 |
 |
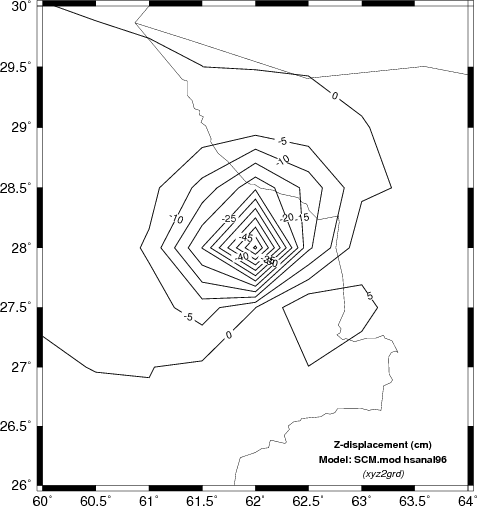
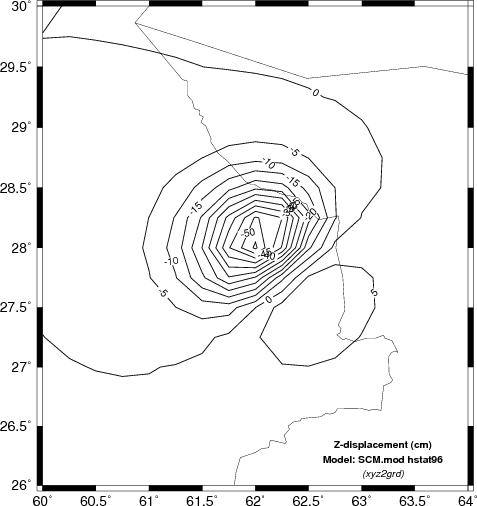
To see the effect of sampling and the difference between the xyz2grd
and surface output compare the following two figures
to those above. In this case the grid interval in latitude
and longitude was 0.5 degrees, which yielded a 9x9 grid. The
program surface smooths to a 0.25 degree grid. The
difference in computational effort is roughly a factor of 4, e.g.,
(17x17)/(9x9), the number of grid locations.
| Vertical
deformation (cm) determined using a coarser sampling grid |
|
 |
 |
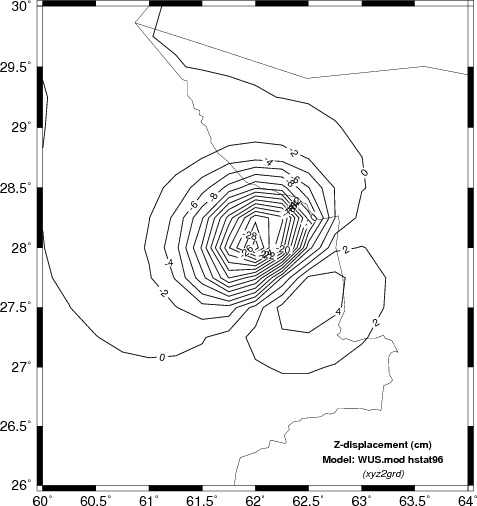
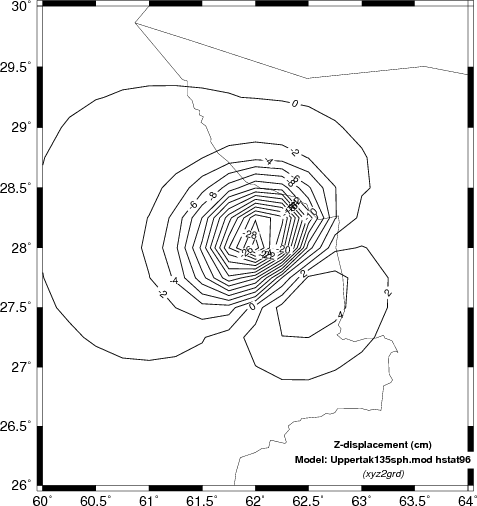
The second test is to investigate the sensitivity of the finite
fault solution to the velocity model used.
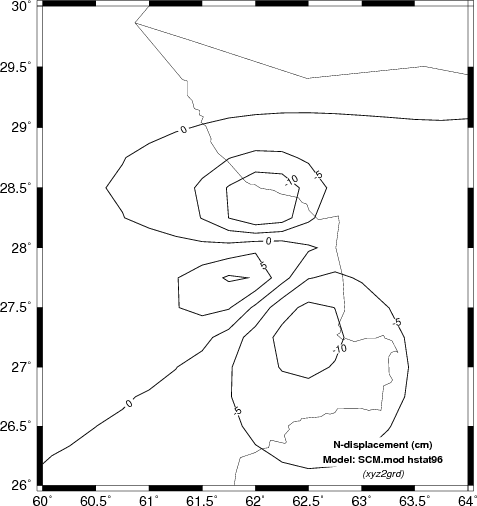
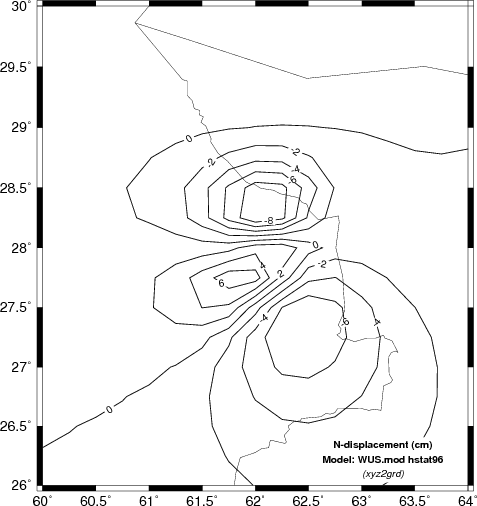
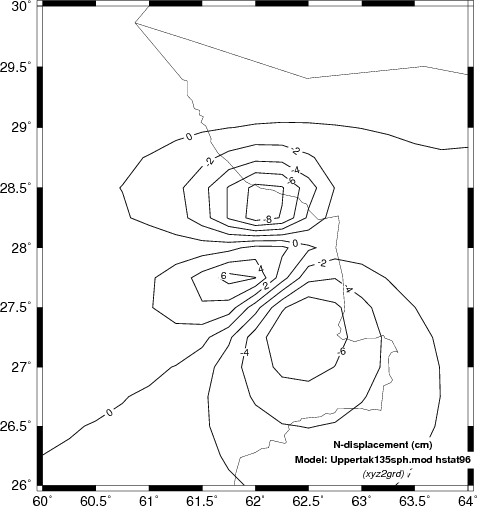
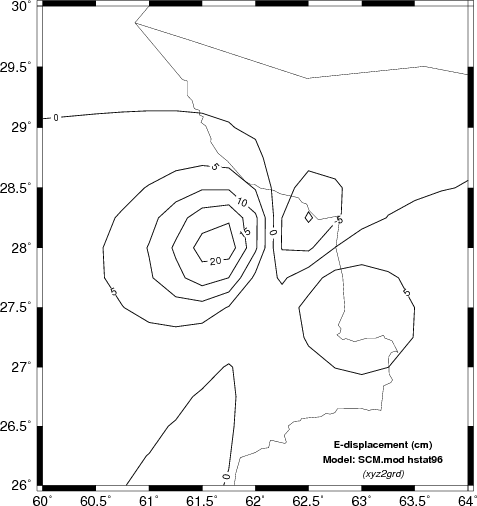
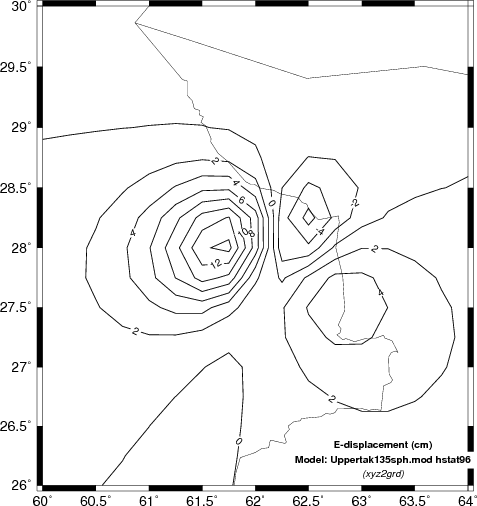
Here we will compare the computed displacements in the N (north) E
(east) and Z (up directions). In the case of the Z comparison
we are able to compare the results to INSAR estimates.
Comparison of vertical component deformation (cm) for the SCM, WUS and upper AK135 velocity models. These are compared |
|
 ` |
 ` |
 ` |
 |
|
|
 |
 |
 |
|
|
|
 |
 |
 |
|
The obvious difference among the predicted static displacements as a function of the velocity models is that the simple halfspace model predicts the highest amplitudes. This is not surprising since the theoretical amplitude is a function of the ratio (seismic moment)/rigidity. The velocity at the source depth in the simple model is the least, and hence the predicted amplitudes are the greatest.
Since we are discussing the static deformation due to a rupturing finite fault, an interesting question concerns how the static deformation builds or when has the final static offset been achieved. As an approximation we assume here that the static offset is coincident with the first S-wave arrival. The link compares this assumption to a simulation that scales, shifts and adds complete regional seismograms. Comparison of displacement time histories.
Hopefully there may be some value in this presentation in addition to demonstrating how this can be done using these codes.
Avinash Nayak found an error in this documentation.