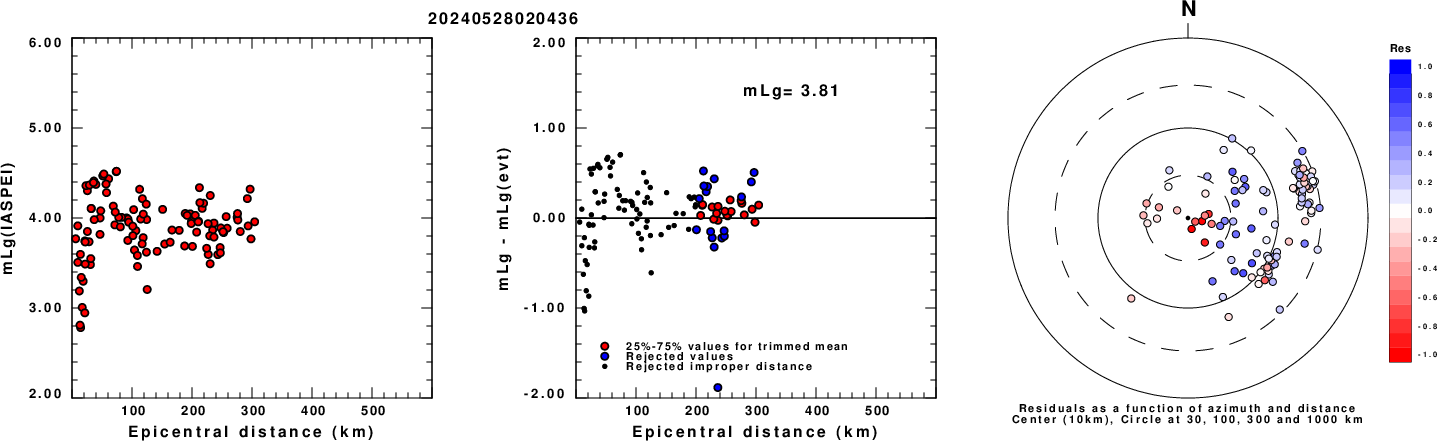
Left: mLg computed using the IASPEI formula. Center: mLg residuals versus epicentral distance ; the values used for the trimmed mean magnitude estimate are indicated. Right: residuals as a function of distance and azimuth.
The ANSS event ID is tx2024kkoo and the event page is at https://earthquake.usgs.gov/earthquakes/eventpage/tx2024kkoo/executive.
2024/05/28 02:04:36 31.681 -104.201 8.9 3.9 Texas
USGS/SLU Moment Tensor Solution
ENS 2024/05/28 02:04:36:0 31.68 -104.20 8.9 3.9 Texas
Stations used:
4O.BP01 4O.CV01 4O.DB02 4O.DB03 4O.DB04 4O.LWM1 4O.MBBB2
4O.MID01 4O.MID02 4O.MID03 4O.SA07 4O.SA09 4O.VW01 4O.WB03
4O.WB04 4O.WB05 4O.WB06 4O.WB07 4O.WB10 4O.WB11 4O.WB12
4T.NM01 4T.NM02 TX.ALPN TX.MB07 TX.MB16 TX.MB25 TX.MNHN
TX.ODSA TX.PB01 TX.PB03 TX.PB04 TX.PB05 TX.PB06 TX.PB07
TX.PB09 TX.PB10 TX.PB11 TX.PB12 TX.PB13 TX.PB14 TX.PB16
TX.PB17 TX.PB18 TX.PB19 TX.PB21 TX.PB22 TX.PB24 TX.PB26
TX.PB28 TX.PB29 TX.PB30 TX.PB31 TX.PB35 TX.PB37 TX.PB38
TX.PB43 TX.PB46 TX.PB51 TX.PB54 TX.PCOS TX.PECS TX.VHRN
Filtering commands used:
cut o DIST/3.3 -40 o DIST/3.3 +50
rtr
taper w 0.1
hp c 0.03 n 3
lp c 0.20 n 3
Best Fitting Double Couple
Mo = 4.79e+21 dyne-cm
Mw = 3.72
Z = 8 km
Plane Strike Dip Rake
NP1 97 69 -103
NP2 310 25 -60
Principal Axes:
Axis Value Plunge Azimuth
T 4.79e+21 22 197
N 0.00e+00 12 102
P -4.79e+21 64 346
Moment Tensor: (dyne-cm)
Component Value
Mxx 2.86e+21
Mxy 1.39e+21
Mxz -3.44e+21
Myy 3.16e+20
Myz -5.11e+19
Mzz -3.18e+21
##############
######################
##----------------##########
-----------------------#######
---------------------------#######
------------------------------######
---------------- --------------#####
----------------- P ---------------#####
----------------- ----------------####
--------------------------------------####
##------------------------------------####
#####----------------------------------###
#########------------------------------##-
###############---------------------##--
######################################--
#####################################-
###################################-
##################################
######### ##################
######## T #################
##### ##############
##############
Global CMT Convention Moment Tensor:
R T P
-3.18e+21 -3.44e+21 5.11e+19
-3.44e+21 2.86e+21 -1.39e+21
5.11e+19 -1.39e+21 3.16e+20
Details of the solution is found at
http://www.eas.slu.edu/eqc/eqc_mt/MECH.NA/20240528020436/index.html
|
STK = 310
DIP = 25
RAKE = -60
MW = 3.72
HS = 8.0
The NDK file is 20240528020436.ndk The waveform inversion is preferred.
Given the availability of digital waveforms for determination of the moment tensor, this section documents the added processing leading to mLg, if appropriate to the region, and ML by application of the respective IASPEI formulae. As a research study, the linear distance term of the IASPEI formula for ML is adjusted to remove a linear distance trend in residuals to give a regionally defined ML. The defined ML uses horizontal component recordings, but the same procedure is applied to the vertical components since there may be some interest in vertical component ground motions. Residual plots versus distance may indicate interesting features of ground motion scaling in some distance ranges. A residual plot of the regionalized magnitude is given as a function of distance and azimuth, since data sets may transcend different wave propagation provinces.

Left: mLg computed using the IASPEI formula. Center: mLg residuals versus epicentral distance ; the values used for the trimmed mean magnitude estimate are indicated.
Right: residuals as a function of distance and azimuth.
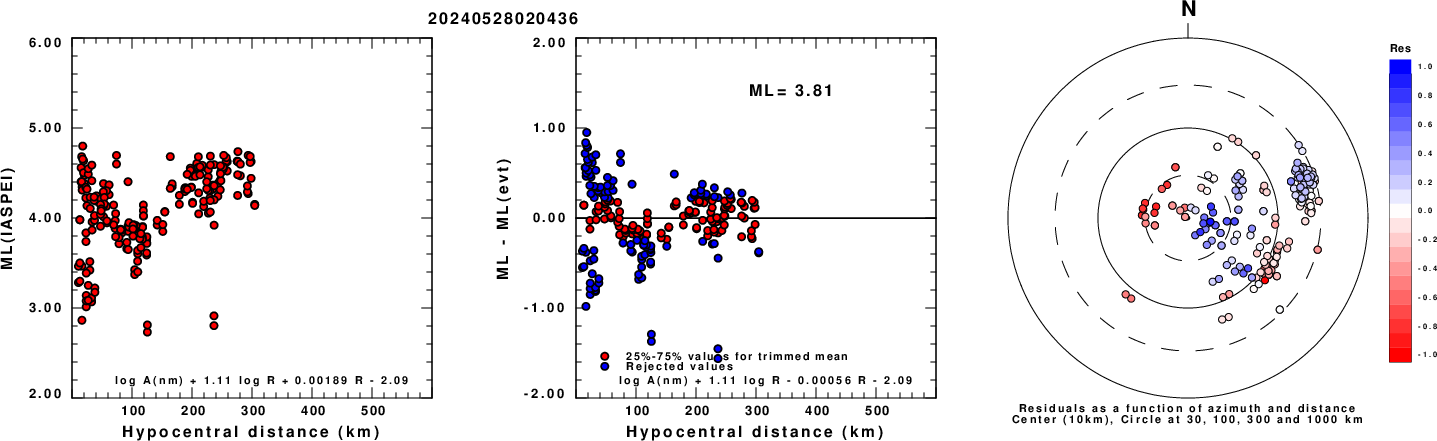
Left: ML computed using the IASPEI formula for Horizontal components. Center: ML residuals computed using a modified IASPEI formula that accounts for path specific attenuation; the values used for the trimmed mean are indicated. The ML relation used for each figure is given at the bottom of each plot.
Right: Residuals from new relation as a function of distance and azimuth.
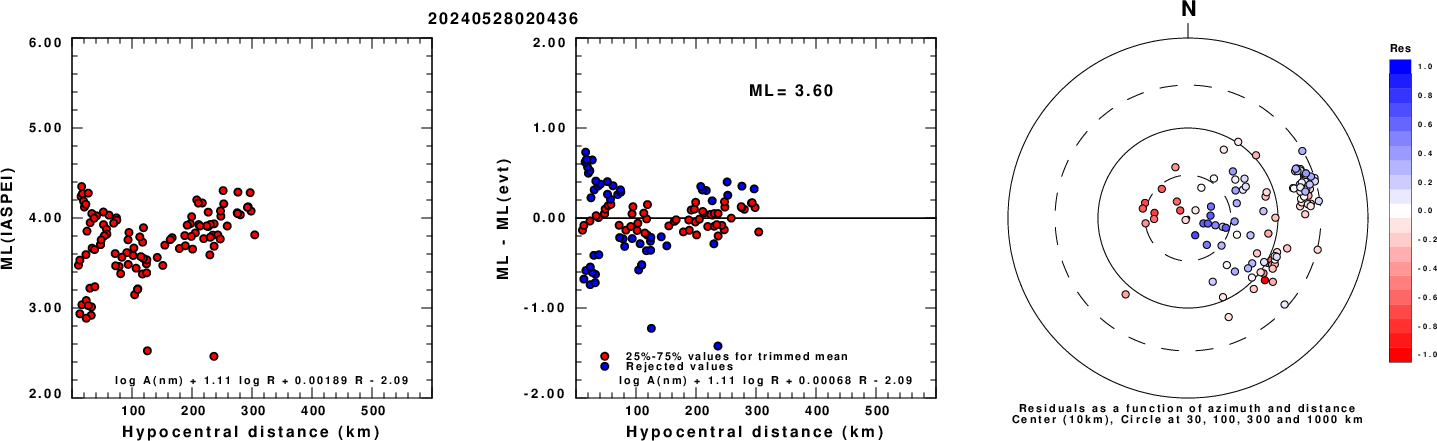
Left: ML computed using the IASPEI formula for Vertical components (research). Center: ML residuals computed using a modified IASPEI formula that accounts for path specific attenuation; the values used for the trimmed mean are indicated. The ML relation used for each figure is given at the bottom of each plot.
Right: Residuals from new relation as a function of distance and azimuth.
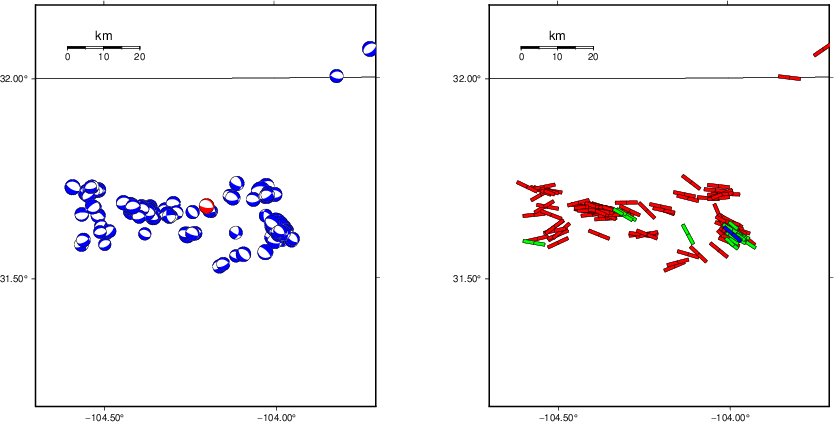 |
The focal mechanism was determined using broadband seismic waveforms. The location of the event (star) and the stations used for (red) the waveform inversion are shown in the next figure.
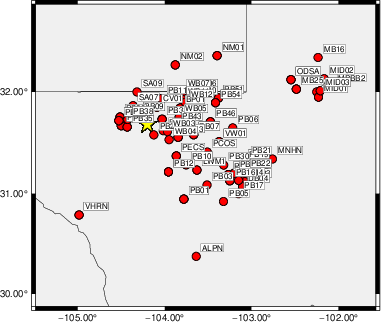
|
|
|
The program wvfgrd96 was used with good traces observed at short distance to determine the focal mechanism, depth and seismic moment. This technique requires a high quality signal and well determined velocity model for the Green's functions. To the extent that these are the quality data, this type of mechanism should be preferred over the radiation pattern technique which requires the separate step of defining the pressure and tension quadrants and the correct strike.
The observed and predicted traces are filtered using the following gsac commands:
cut o DIST/3.3 -40 o DIST/3.3 +50 rtr taper w 0.1 hp c 0.03 n 3 lp c 0.20 n 3The results of this grid search are as follow:
DEPTH STK DIP RAKE MW FIT
WVFGRD96 1.0 265 70 0 3.00 0.1449
WVFGRD96 2.0 260 50 -10 3.24 0.1900
WVFGRD96 3.0 100 75 85 3.40 0.2631
WVFGRD96 4.0 305 20 -65 3.47 0.3712
WVFGRD96 5.0 305 25 -65 3.53 0.4503
WVFGRD96 6.0 310 30 -60 3.58 0.4991
WVFGRD96 7.0 315 30 -55 3.62 0.5216
WVFGRD96 8.0 310 25 -60 3.72 0.5240
WVFGRD96 9.0 310 25 -60 3.76 0.5197
WVFGRD96 10.0 315 25 -60 3.78 0.5010
WVFGRD96 11.0 320 25 -55 3.80 0.4704
WVFGRD96 12.0 325 25 -50 3.82 0.4319
WVFGRD96 13.0 335 25 -40 3.83 0.3913
WVFGRD96 14.0 340 25 -35 3.84 0.3536
WVFGRD96 15.0 350 25 -20 3.85 0.3205
WVFGRD96 16.0 355 25 -15 3.85 0.2907
WVFGRD96 17.0 0 20 -10 3.85 0.2655
WVFGRD96 18.0 15 20 10 3.85 0.2451
WVFGRD96 19.0 50 25 40 3.85 0.2354
WVFGRD96 20.0 55 25 45 3.86 0.2341
WVFGRD96 21.0 65 25 55 3.86 0.2327
WVFGRD96 22.0 65 25 55 3.87 0.2315
WVFGRD96 23.0 300 50 -75 3.84 0.2315
WVFGRD96 24.0 300 50 -75 3.84 0.2346
WVFGRD96 25.0 300 50 -75 3.84 0.2345
WVFGRD96 26.0 85 40 50 3.85 0.2320
WVFGRD96 27.0 85 40 50 3.86 0.2316
WVFGRD96 28.0 85 40 45 3.86 0.2284
WVFGRD96 29.0 90 40 50 3.85 0.2244
The best solution is
WVFGRD96 8.0 310 25 -60 3.72 0.5240
The mechanism corresponding to the best fit is
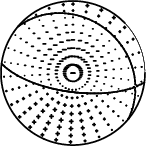
|
|
|
The best fit as a function of depth is given in the following figure:
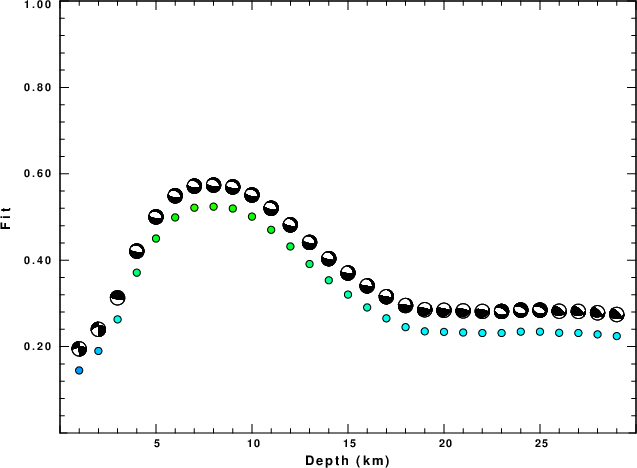
|
|
|
The comparison of the observed and predicted waveforms is given in the next figure. The red traces are the observed and the blue are the predicted. Each observed-predicted component is plotted to the same scale and peak amplitudes are indicated by the numbers to the left of each trace. A pair of numbers is given in black at the right of each predicted traces. The upper number it the time shift required for maximum correlation between the observed and predicted traces. This time shift is required because the synthetics are not computed at exactly the same distance as the observed, the velocity model used in the predictions may not be perfect and the epicentral parameters may be be off. A positive time shift indicates that the prediction is too fast and should be delayed to match the observed trace (shift to the right in this figure). A negative value indicates that the prediction is too slow. The lower number gives the percentage of variance reduction to characterize the individual goodness of fit (100% indicates a perfect fit).
The bandpass filter used in the processing and for the display was
cut o DIST/3.3 -40 o DIST/3.3 +50 rtr taper w 0.1 hp c 0.03 n 3 lp c 0.20 n 3

|
| Figure 3. Waveform comparison for selected depth. Red: observed; Blue - predicted. The time shift with respect to the model prediction is indicated. The percent of fit is also indicated. The time scale is relative to the first trace sample. |
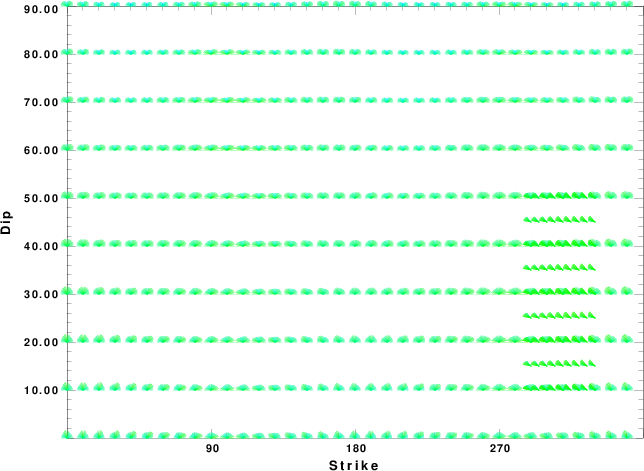
|
| Focal mechanism sensitivity at the preferred depth. The red color indicates a very good fit to the waveforms. Each solution is plotted as a vector at a given value of strike and dip with the angle of the vector representing the rake angle, measured, with respect to the upward vertical (N) in the figure. |
A check on the assumed source location is possible by looking at the time shifts between the observed and predicted traces. The time shifts for waveform matching arise for several reasons:
Time_shift = A + B cos Azimuth + C Sin Azimuth
The time shifts for this inversion lead to the next figure:
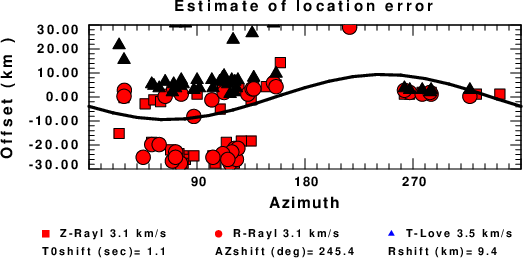
The derived shift in origin time and epicentral coordinates are given at the bottom of the figure.
The WUS.model used for the waveform synthetic seismograms and for the surface wave eigenfunctions and dispersion is as follows (The format is in the model96 format of Computer Programs in Seismology).
MODEL.01
Model after 8 iterations
ISOTROPIC
KGS
FLAT EARTH
1-D
CONSTANT VELOCITY
LINE08
LINE09
LINE10
LINE11
H(KM) VP(KM/S) VS(KM/S) RHO(GM/CC) QP QS ETAP ETAS FREFP FREFS
1.9000 3.4065 2.0089 2.2150 0.302E-02 0.679E-02 0.00 0.00 1.00 1.00
6.1000 5.5445 3.2953 2.6089 0.349E-02 0.784E-02 0.00 0.00 1.00 1.00
13.0000 6.2708 3.7396 2.7812 0.212E-02 0.476E-02 0.00 0.00 1.00 1.00
19.0000 6.4075 3.7680 2.8223 0.111E-02 0.249E-02 0.00 0.00 1.00 1.00
0.0000 7.9000 4.6200 3.2760 0.164E-10 0.370E-10 0.00 0.00 1.00 1.00