Location
Location ANSS
The ANSS event ID is ak022ddfhisv and the event page is at
https://earthquake.usgs.gov/earthquakes/eventpage/ak022ddfhisv/executive.
2022/10/18 10:24:26 61.375 -149.818 28.8 3.6 Alaska
Focal Mechanism
USGS/SLU Moment Tensor Solution
ENS 2022/10/18 10:24:26:0 61.38 -149.82 28.8 3.6 Alaska
Stations used:
AK.FID AK.FIRE AK.GHO AK.GLI AK.KNK AK.L22K AK.PWL AK.RC01
AK.SAW AK.SSN AT.PMR AV.RED AV.SPCP
Filtering commands used:
cut o DIST/3.3 -40 o DIST/3.3 +50
rtr
taper w 0.1
hp c 0.03 n 3
lp c 0.10 n 3
br c 0.12 0.25 n 4 p 2
Best Fitting Double Couple
Mo = 6.76e+21 dyne-cm
Mw = 3.82
Z = 40 km
Plane Strike Dip Rake
NP1 200 75 -60
NP2 314 33 -152
Principal Axes:
Axis Value Plunge Azimuth
T 6.76e+21 24 267
N 0.00e+00 29 11
P -6.76e+21 51 144
Moment Tensor: (dyne-cm)
Component Value
Mxx -1.76e+21
Mxy 1.56e+21
Mxz 2.56e+21
Myy 4.68e+21
Myz -4.47e+21
Mzz -2.93e+21
--------------
----------------######
--############----##########
#################--###########
##################------##########
##################----------########
##################------------########
##################---------------#######
##################----------------######
##################------------------######
#### ##########--------------------#####
#### T ##########--------------------#####
#### #########----------------------####
###############----------------------###
##############---------- ----------###
#############---------- P ----------##
###########----------- ---------##
##########-----------------------#
########----------------------
#######---------------------
####------------------
--------------
Global CMT Convention Moment Tensor:
R T P
-2.93e+21 2.56e+21 4.47e+21
2.56e+21 -1.76e+21 -1.56e+21
4.47e+21 -1.56e+21 4.68e+21
Details of the solution is found at
http://www.eas.slu.edu/eqc/eqc_mt/MECH.NA/20221018102426/index.html
|
Preferred Solution
The preferred solution from an analysis of the surface-wave spectral amplitude radiation pattern, waveform inversion or first motion observations is
STK = 200
DIP = 75
RAKE = -60
MW = 3.82
HS = 40.0
The NDK file is 20221018102426.ndk
The waveform inversion is preferred.
Magnitudes
Given the availability of digital waveforms for determination of the moment tensor, this section documents the added processing leading to mLg, if appropriate to the region, and ML by application of the respective IASPEI formulae. As a research study, the linear distance term of the IASPEI formula
for ML is adjusted to remove a linear distance trend in residuals to give a regionally defined ML. The defined ML uses horizontal component recordings, but the same procedure is applied to the vertical components since there may be some interest in vertical component ground motions. Residual plots versus distance may indicate interesting features of ground motion scaling in some distance ranges. A residual plot of the regionalized magnitude is given as a function of distance and azimuth, since data sets may transcend different wave propagation provinces.
ML Magnitude
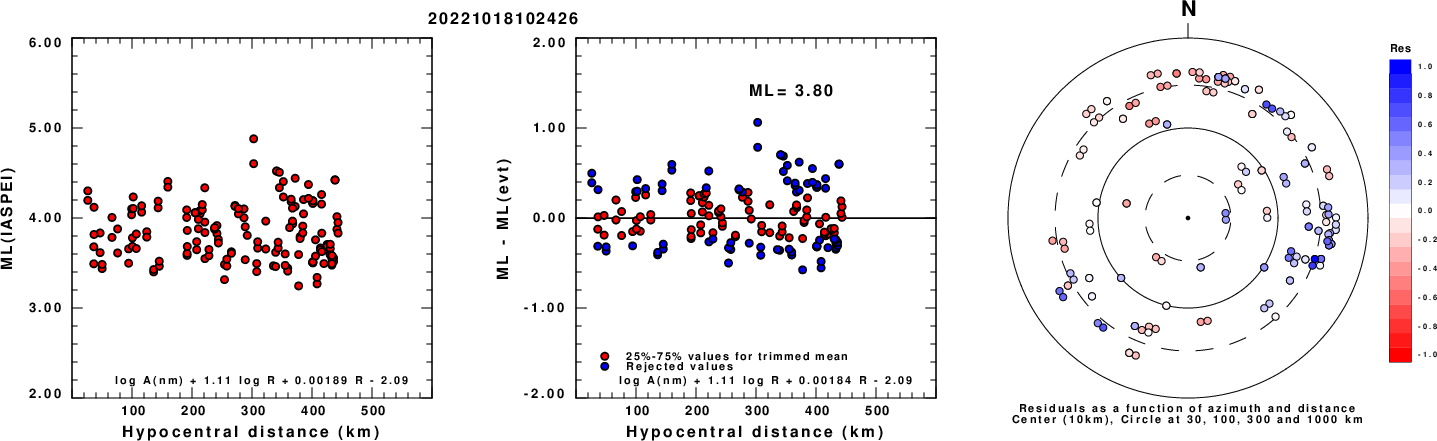
Left: ML computed using the IASPEI formula for Horizontal components. Center: ML residuals computed using a modified IASPEI formula that accounts for path specific attenuation; the values used for the trimmed mean are indicated. The ML relation used for each figure is given at the bottom of each plot.
Right: Residuals from new relation as a function of distance and azimuth.
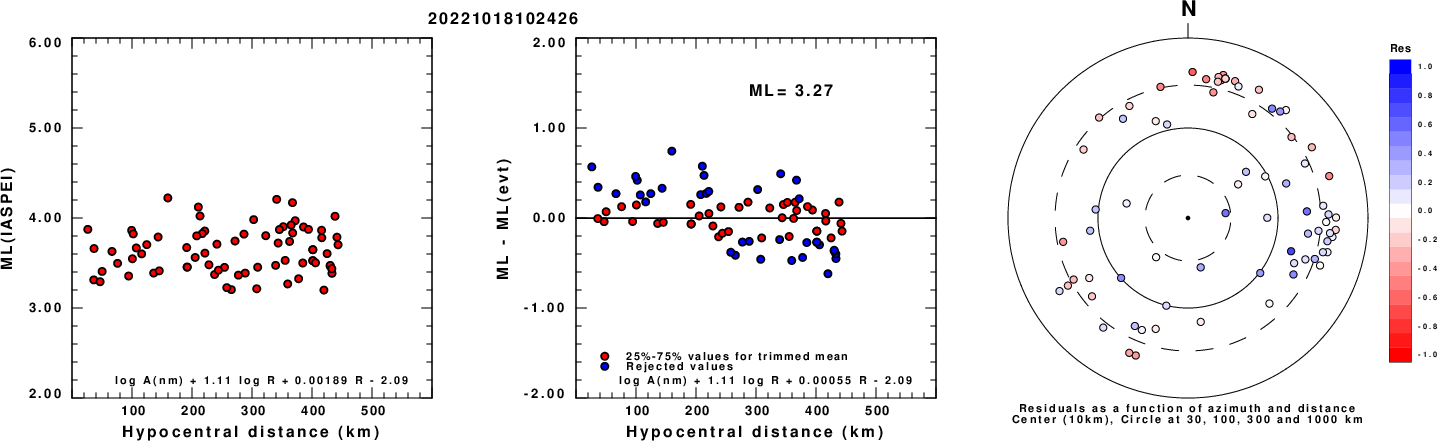
Left: ML computed using the IASPEI formula for Vertical components (research). Center: ML residuals computed using a modified IASPEI formula that accounts for path specific attenuation; the values used for the trimmed mean are indicated. The ML relation used for each figure is given at the bottom of each plot.
Right: Residuals from new relation as a function of distance and azimuth.
Context
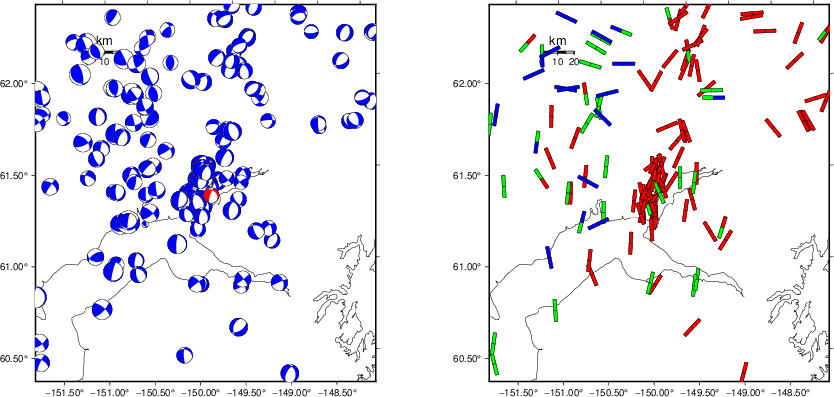
The left panel of the next figure presents the focal mechanism for this earthquake (red) in the context of other nearby events (blue) in the SLU Moment Tensor Catalog. The right panel shows the inferred direction of maximum compressive stress and the type of faulting (green is strike-slip, red is normal, blue is thrust; oblique is shown by a combination of colors). Thus context plot is useful for assessing the appropriateness of the moment tensor of this event.
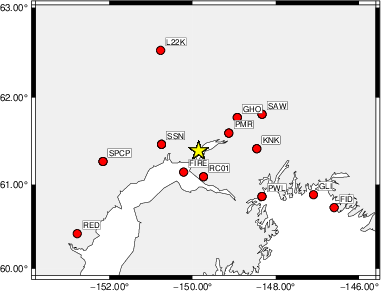
Waveform Inversion using wvfgrd96
The focal mechanism was determined using broadband seismic waveforms. The location of the event (star) and the
stations used for (red) the waveform inversion are shown in the next figure.
|
|
Location of broadband stations used for waveform inversion
|
The program wvfgrd96 was used with good traces observed at short distance to determine the focal mechanism, depth and seismic moment. This technique requires a high quality signal and well determined velocity model for the Green's functions. To the extent that these are the quality data, this type of mechanism should be preferred over the radiation pattern technique which requires the separate step of defining the pressure and tension quadrants and the correct strike.
The observed and predicted traces are filtered using the following gsac commands:
cut o DIST/3.3 -40 o DIST/3.3 +50
rtr
taper w 0.1
hp c 0.03 n 3
lp c 0.10 n 3
br c 0.12 0.25 n 4 p 2
The results of this grid search are as follow:
DEPTH STK DIP RAKE MW FIT
WVFGRD96 2.0 40 70 -20 3.19 0.3414
WVFGRD96 4.0 40 80 -15 3.30 0.4150
WVFGRD96 6.0 35 75 25 3.39 0.4447
WVFGRD96 8.0 45 60 35 3.46 0.4736
WVFGRD96 10.0 45 65 25 3.46 0.4928
WVFGRD96 12.0 45 70 25 3.48 0.5059
WVFGRD96 14.0 45 70 25 3.50 0.5157
WVFGRD96 16.0 45 70 25 3.52 0.5220
WVFGRD96 18.0 45 70 25 3.54 0.5284
WVFGRD96 20.0 40 85 40 3.56 0.5395
WVFGRD96 22.0 40 85 40 3.58 0.5532
WVFGRD96 24.0 40 85 40 3.60 0.5650
WVFGRD96 26.0 210 75 -45 3.62 0.5777
WVFGRD96 28.0 210 75 -45 3.64 0.5973
WVFGRD96 30.0 210 75 -50 3.65 0.6113
WVFGRD96 32.0 210 80 -50 3.67 0.6286
WVFGRD96 34.0 205 75 -50 3.68 0.6419
WVFGRD96 36.0 205 75 -50 3.70 0.6504
WVFGRD96 38.0 200 75 -50 3.72 0.6498
WVFGRD96 40.0 200 75 -60 3.82 0.6579
WVFGRD96 42.0 195 70 -60 3.83 0.6556
WVFGRD96 44.0 195 70 -60 3.84 0.6515
WVFGRD96 46.0 195 70 -60 3.85 0.6455
WVFGRD96 48.0 195 70 -60 3.86 0.6399
WVFGRD96 50.0 190 70 -60 3.88 0.6330
WVFGRD96 52.0 195 75 -55 3.89 0.6275
WVFGRD96 54.0 195 75 -55 3.89 0.6203
WVFGRD96 56.0 190 75 -55 3.92 0.6136
WVFGRD96 58.0 190 75 -55 3.92 0.6071
WVFGRD96 60.0 190 75 -55 3.93 0.5996
WVFGRD96 62.0 190 75 -55 3.93 0.5925
WVFGRD96 64.0 190 75 -55 3.94 0.5850
WVFGRD96 66.0 190 75 -55 3.94 0.5771
WVFGRD96 68.0 190 75 -55 3.95 0.5689
WVFGRD96 70.0 190 75 -55 3.95 0.5606
WVFGRD96 72.0 30 70 40 3.98 0.5474
WVFGRD96 74.0 30 70 40 3.99 0.5493
WVFGRD96 76.0 30 70 40 3.99 0.5511
WVFGRD96 78.0 30 70 40 4.00 0.5527
WVFGRD96 80.0 30 70 40 4.00 0.5530
WVFGRD96 82.0 30 70 40 4.01 0.5499
WVFGRD96 84.0 30 70 40 4.01 0.5452
WVFGRD96 86.0 30 70 40 4.01 0.5403
WVFGRD96 88.0 30 70 35 4.02 0.5375
WVFGRD96 90.0 30 70 35 4.03 0.5339
WVFGRD96 92.0 30 70 35 4.03 0.5267
WVFGRD96 94.0 25 75 30 4.04 0.5147
WVFGRD96 96.0 25 80 30 4.03 0.5036
WVFGRD96 98.0 30 75 25 4.03 0.4925
The best solution is
WVFGRD96 40.0 200 75 -60 3.82 0.6579
The mechanism corresponding to the best fit is
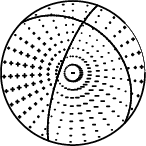
|
|
Figure 1. Waveform inversion focal mechanism
|
The best fit as a function of depth is given in the following figure:
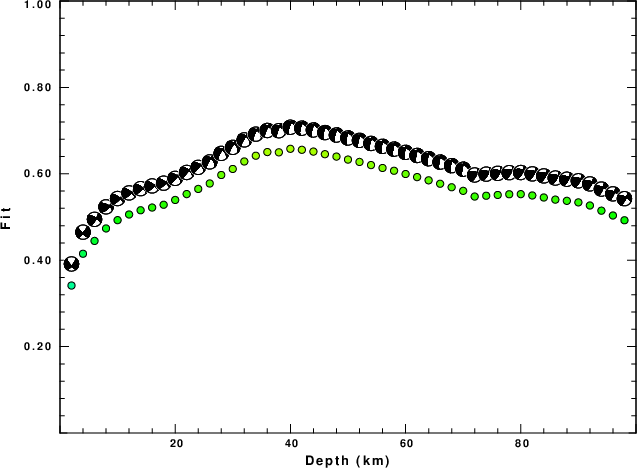
|
|
Figure 2. Depth sensitivity for waveform mechanism
|
The comparison of the observed and predicted waveforms is given in the next figure. The red traces are the observed and the blue are the predicted.
Each observed-predicted component is plotted to the same scale and peak amplitudes are indicated by the numbers to the left of each trace. A pair of numbers is given in black at the right of each predicted traces. The upper number it the time shift required for maximum correlation between the observed and predicted traces. This time shift is required because the synthetics are not computed at exactly the same distance as the observed, the velocity model used in the predictions may not be perfect and the epicentral parameters may be be off.
A positive time shift indicates that the prediction is too fast and should be delayed to match the observed trace (shift to the right in this figure). A negative value indicates that the prediction is too slow. The lower number gives the percentage of variance reduction to characterize the individual goodness of fit (100% indicates a perfect fit).
The bandpass filter used in the processing and for the display was
cut o DIST/3.3 -40 o DIST/3.3 +50
rtr
taper w 0.1
hp c 0.03 n 3
lp c 0.10 n 3
br c 0.12 0.25 n 4 p 2
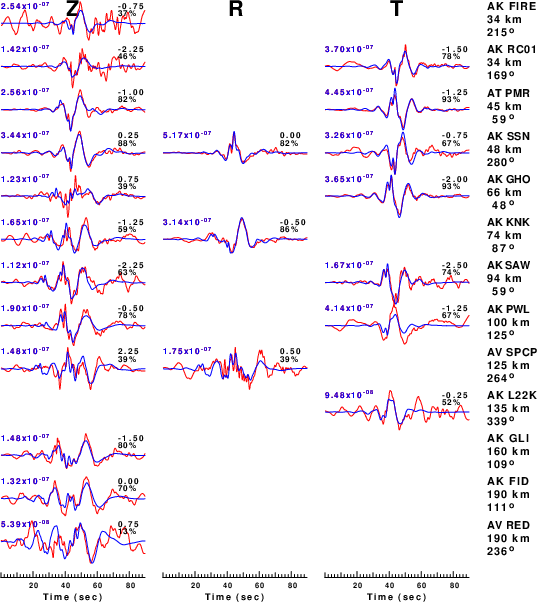
|
|
Figure 3. Waveform comparison for selected depth. Red: observed; Blue - predicted. The time shift with respect to the model prediction is indicated. The percent of fit is also indicated. The time scale is relative to the first trace sample.
|
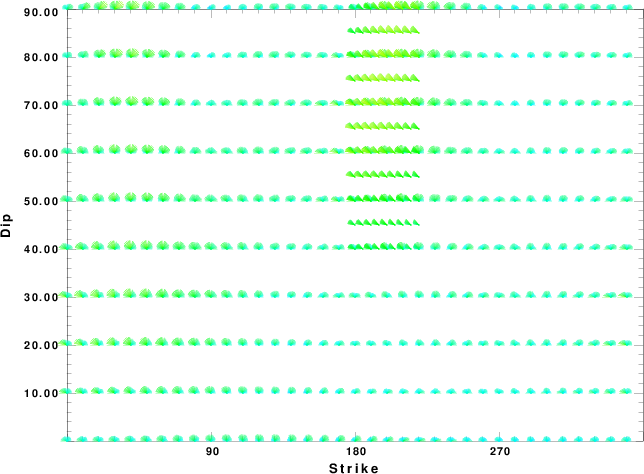
|
|
Focal mechanism sensitivity at the preferred depth. The red color indicates a very good fit to the waveforms.
Each solution is plotted as a vector at a given value of strike and dip with the angle of the vector representing the rake angle, measured, with respect to the upward vertical (N) in the figure.
|
A check on the assumed source location is possible by looking at the time shifts between the observed and predicted traces. The time shifts for waveform matching arise for several reasons:
- The origin time and epicentral distance are incorrect
- The velocity model used for the inversion is incorrect
- The velocity model used to define the P-arrival time is not the
same as the velocity model used for the waveform inversion
(assuming that the initial trace alignment is based on the
P arrival time)
Assuming only a mislocation, the time shifts are fit to a functional form:
Time_shift = A + B cos Azimuth + C Sin Azimuth
The time shifts for this inversion lead to the next figure:
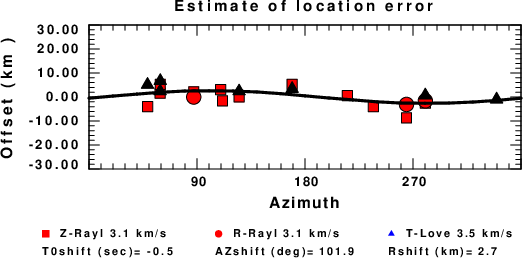
The derived shift in origin time and epicentral coordinates are given at the bottom of the figure.
Velocity Model
The WUS.model used for the waveform synthetic seismograms and for the surface wave eigenfunctions and dispersion is as follows
(The format is in the model96 format of Computer Programs in Seismology).
MODEL.01
Model after 8 iterations
ISOTROPIC
KGS
FLAT EARTH
1-D
CONSTANT VELOCITY
LINE08
LINE09
LINE10
LINE11
H(KM) VP(KM/S) VS(KM/S) RHO(GM/CC) QP QS ETAP ETAS FREFP FREFS
1.9000 3.4065 2.0089 2.2150 0.302E-02 0.679E-02 0.00 0.00 1.00 1.00
6.1000 5.5445 3.2953 2.6089 0.349E-02 0.784E-02 0.00 0.00 1.00 1.00
13.0000 6.2708 3.7396 2.7812 0.212E-02 0.476E-02 0.00 0.00 1.00 1.00
19.0000 6.4075 3.7680 2.8223 0.111E-02 0.249E-02 0.00 0.00 1.00 1.00
0.0000 7.9000 4.6200 3.2760 0.164E-10 0.370E-10 0.00 0.00 1.00 1.00
Last Changed Thu Apr 25 02:15:59 AM CDT 2024