Location
Location ANSS
The ANSS event ID is ak0141fma9kq and the event page is at
https://earthquake.usgs.gov/earthquakes/eventpage/ak0141fma9kq/executive.
2014/01/31 21:20:54 58.118 -151.755 49.2 4.2 Alaska
Focal Mechanism
USGS/SLU Moment Tensor Solution
ENS 2014/01/31 21:20:54:0 58.12 -151.76 49.2 4.2 Alaska
Stations used:
AK.BRLK AK.BRSE AK.CNP AK.EYAK AK.FID AK.GHO AK.HOM AK.PWL
AK.WAT1 AT.OHAK AT.PMR AT.SVW2 AT.TTA II.KDAK
Filtering commands used:
cut a -30 a 180
rtr
taper w 0.1
hp c 0.02 n 3
lp c 0.06 n 3
Best Fitting Double Couple
Mo = 2.19e+22 dyne-cm
Mw = 4.16
Z = 41 km
Plane Strike Dip Rake
NP1 335 90 -150
NP2 245 60 0
Principal Axes:
Axis Value Plunge Azimuth
T 2.19e+22 21 106
N 0.00e+00 60 335
P -2.19e+22 21 204
Moment Tensor: (dyne-cm)
Component Value
Mxx -1.45e+22
Mxy -1.22e+22
Mxz 4.62e+21
Myy 1.45e+22
Myz 9.91e+21
Mzz 0.00e+00
--------------
###-------------------
#######---------------------
#########---------------------
###########-----------------------
#############--------------####-----
###############----###################
################-#######################
#############-----######################
###########---------######################
#########------------#####################
#######--------------#####################
#####-----------------############## ###
###-------------------############# T ##
##---------------------############ ##
-----------------------###############
-----------------------#############
-----------------------###########
------- -----------#########
------ P ------------#######
--- -------------###
--------------
Global CMT Convention Moment Tensor:
R T P
0.00e+00 4.62e+21 -9.91e+21
4.62e+21 -1.45e+22 1.22e+22
-9.91e+21 1.22e+22 1.45e+22
Details of the solution is found at
http://www.eas.slu.edu/eqc/eqc_mt/MECH.NA/20140131212054/index.html
|
Preferred Solution
The preferred solution from an analysis of the surface-wave spectral amplitude radiation pattern, waveform inversion or first motion observations is
STK = 245
DIP = 60
RAKE = 0
MW = 4.16
HS = 41.0
The NDK file is 20140131212054.ndk
The waveform inversion is preferred.
Moment Tensor Comparison
The following compares this source inversion to those provided by others. The purpose is to look for major differences and also to note slight differences that might be inherent to the processing procedure. For completeness the USGS/SLU solution is repeated from above.
| SLU |
USGSMT |
USGS/SLU Moment Tensor Solution
ENS 2014/01/31 21:20:54:0 58.12 -151.76 49.2 4.2 Alaska
Stations used:
AK.BRLK AK.BRSE AK.CNP AK.EYAK AK.FID AK.GHO AK.HOM AK.PWL
AK.WAT1 AT.OHAK AT.PMR AT.SVW2 AT.TTA II.KDAK
Filtering commands used:
cut a -30 a 180
rtr
taper w 0.1
hp c 0.02 n 3
lp c 0.06 n 3
Best Fitting Double Couple
Mo = 2.19e+22 dyne-cm
Mw = 4.16
Z = 41 km
Plane Strike Dip Rake
NP1 335 90 -150
NP2 245 60 0
Principal Axes:
Axis Value Plunge Azimuth
T 2.19e+22 21 106
N 0.00e+00 60 335
P -2.19e+22 21 204
Moment Tensor: (dyne-cm)
Component Value
Mxx -1.45e+22
Mxy -1.22e+22
Mxz 4.62e+21
Myy 1.45e+22
Myz 9.91e+21
Mzz 0.00e+00
--------------
###-------------------
#######---------------------
#########---------------------
###########-----------------------
#############--------------####-----
###############----###################
################-#######################
#############-----######################
###########---------######################
#########------------#####################
#######--------------#####################
#####-----------------############## ###
###-------------------############# T ##
##---------------------############ ##
-----------------------###############
-----------------------#############
-----------------------###########
------- -----------#########
------ P ------------#######
--- -------------###
--------------
Global CMT Convention Moment Tensor:
R T P
0.00e+00 4.62e+21 -9.91e+21
4.62e+21 -1.45e+22 1.22e+22
-9.91e+21 1.22e+22 1.45e+22
Details of the solution is found at
http://www.eas.slu.edu/eqc/eqc_mt/MECH.NA/20140131212054/index.html
|
Regional Moment Tensor (Mwr)
Moment magnitude derived from a moment tensor
inversion of complete waveforms at regional
distances (less than ~8 degrees), generally
used for the analysis of small to moderate
size earthquakes (typically Mw 3.5-6.0)
crust or upper mantle earthquakes.
Moment
2.34e+15 N-m
Magnitude
4.2
Percent DC
90%
Depth
41.0 km
Updated
2014-01-31 21:57:33 UTC
Author
us
Catalog
ak
Contributor
us
Code
us_c000meyf_mwr
Principal Axes
Axis Value Plunge Azimuth
T 2.281 16 290
N 0.108 56 47
P -2.389 28 191
Nodal Planes
Plane Strike Dip Rake
NP1 239 82 -33
NP2 334 58 -171
|
|
Magnitudes
Given the availability of digital waveforms for determination of the moment tensor, this section documents the added processing leading to mLg, if appropriate to the region, and ML by application of the respective IASPEI formulae. As a research study, the linear distance term of the IASPEI formula
for ML is adjusted to remove a linear distance trend in residuals to give a regionally defined ML. The defined ML uses horizontal component recordings, but the same procedure is applied to the vertical components since there may be some interest in vertical component ground motions. Residual plots versus distance may indicate interesting features of ground motion scaling in some distance ranges. A residual plot of the regionalized magnitude is given as a function of distance and azimuth, since data sets may transcend different wave propagation provinces.
ML Magnitude
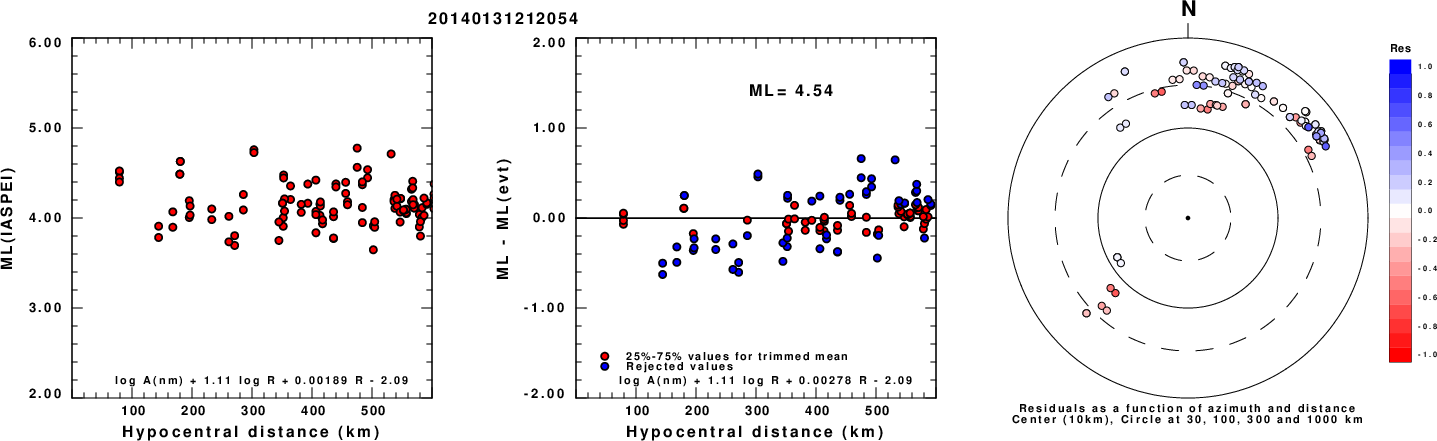
Left: ML computed using the IASPEI formula for Horizontal components. Center: ML residuals computed using a modified IASPEI formula that accounts for path specific attenuation; the values used for the trimmed mean are indicated. The ML relation used for each figure is given at the bottom of each plot.
Right: Residuals from new relation as a function of distance and azimuth.
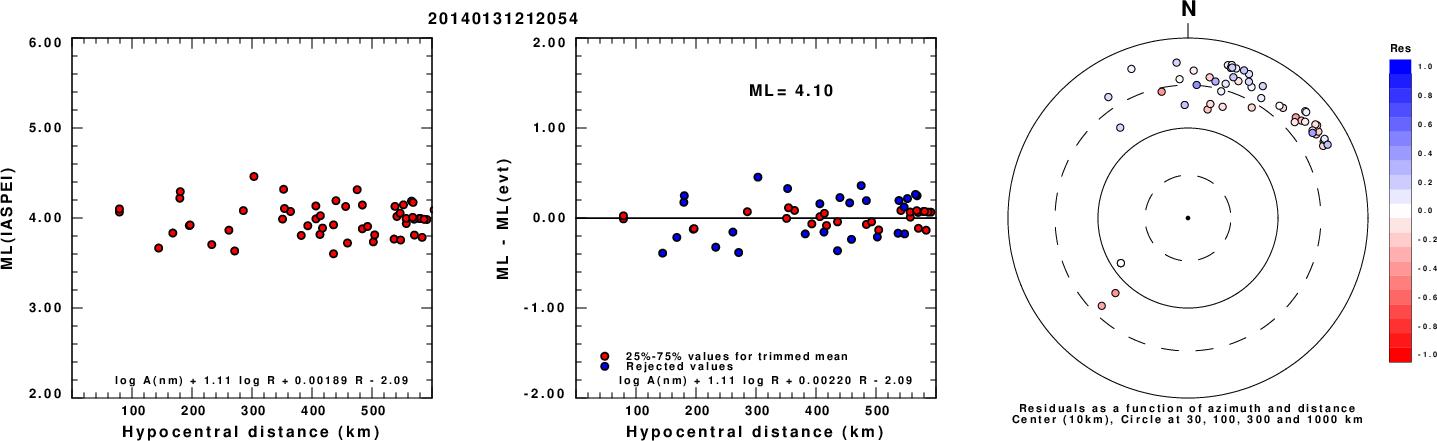
Left: ML computed using the IASPEI formula for Vertical components (research). Center: ML residuals computed using a modified IASPEI formula that accounts for path specific attenuation; the values used for the trimmed mean are indicated. The ML relation used for each figure is given at the bottom of each plot.
Right: Residuals from new relation as a function of distance and azimuth.
Context
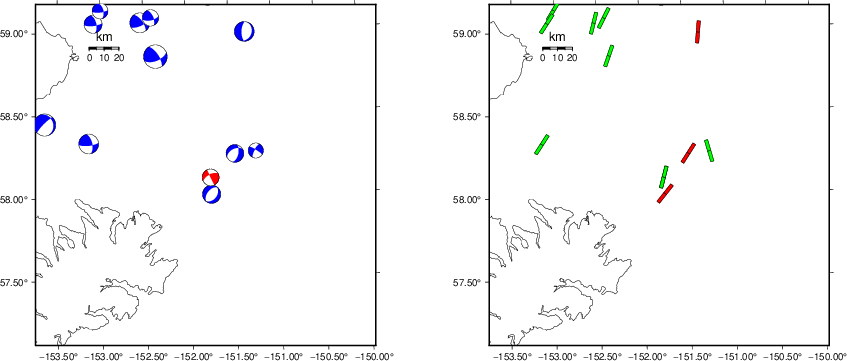
The left panel of the next figure presents the focal mechanism for this earthquake (red) in the context of other nearby events (blue) in the SLU Moment Tensor Catalog. The right panel shows the inferred direction of maximum compressive stress and the type of faulting (green is strike-slip, red is normal, blue is thrust; oblique is shown by a combination of colors). Thus context plot is useful for assessing the appropriateness of the moment tensor of this event.
Waveform Inversion using wvfgrd96
The focal mechanism was determined using broadband seismic waveforms. The location of the event (star) and the
stations used for (red) the waveform inversion are shown in the next figure.
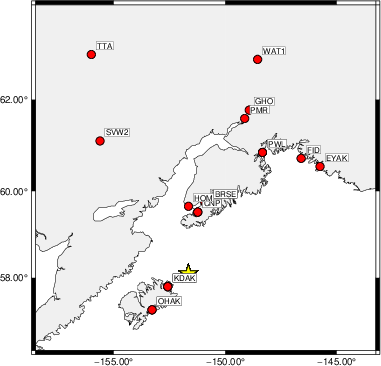
|
|
Location of broadband stations used for waveform inversion
|
The program wvfgrd96 was used with good traces observed at short distance to determine the focal mechanism, depth and seismic moment. This technique requires a high quality signal and well determined velocity model for the Green's functions. To the extent that these are the quality data, this type of mechanism should be preferred over the radiation pattern technique which requires the separate step of defining the pressure and tension quadrants and the correct strike.
The observed and predicted traces are filtered using the following gsac commands:
cut a -30 a 180
rtr
taper w 0.1
hp c 0.02 n 3
lp c 0.06 n 3
The results of this grid search are as follow:
DEPTH STK DIP RAKE MW FIT
WVFGRD96 1.0 20 45 -90 3.59 0.2634
WVFGRD96 3.0 260 55 45 3.65 0.3607
WVFGRD96 5.0 50 55 -10 3.69 0.4145
WVFGRD96 7.0 55 65 0 3.73 0.4676
WVFGRD96 9.0 55 60 -5 3.78 0.4988
WVFGRD96 11.0 55 65 -5 3.81 0.5119
WVFGRD96 13.0 240 65 -15 3.84 0.5363
WVFGRD96 15.0 245 65 -5 3.87 0.5646
WVFGRD96 17.0 245 65 0 3.89 0.5931
WVFGRD96 19.0 245 65 5 3.91 0.6192
WVFGRD96 21.0 245 65 5 3.93 0.6431
WVFGRD96 23.0 245 65 5 3.95 0.6625
WVFGRD96 25.0 245 65 5 3.97 0.6779
WVFGRD96 27.0 245 65 5 3.98 0.6922
WVFGRD96 29.0 245 65 0 4.00 0.7034
WVFGRD96 31.0 245 65 0 4.02 0.7102
WVFGRD96 33.0 245 65 0 4.04 0.7156
WVFGRD96 35.0 245 70 -5 4.07 0.7171
WVFGRD96 37.0 245 70 -5 4.09 0.7199
WVFGRD96 39.0 245 70 -5 4.11 0.7200
WVFGRD96 41.0 245 60 0 4.16 0.7205
WVFGRD96 43.0 245 60 0 4.17 0.7159
WVFGRD96 45.0 245 65 -5 4.20 0.7111
WVFGRD96 47.0 245 65 -5 4.21 0.7026
WVFGRD96 49.0 245 65 -5 4.22 0.6915
WVFGRD96 51.0 245 65 -5 4.23 0.6804
WVFGRD96 53.0 245 65 -5 4.24 0.6679
WVFGRD96 55.0 245 65 -5 4.25 0.6552
WVFGRD96 57.0 245 65 -5 4.26 0.6420
WVFGRD96 59.0 245 65 0 4.25 0.6283
WVFGRD96 61.0 245 65 -5 4.27 0.6154
WVFGRD96 63.0 245 65 0 4.26 0.6023
WVFGRD96 65.0 25 65 -80 4.32 0.5902
WVFGRD96 67.0 30 70 -75 4.31 0.5897
WVFGRD96 69.0 30 70 -75 4.31 0.5889
WVFGRD96 71.0 30 70 -75 4.31 0.5881
WVFGRD96 73.0 30 70 -75 4.31 0.5858
WVFGRD96 75.0 30 70 -75 4.31 0.5829
WVFGRD96 77.0 30 75 -75 4.32 0.5823
WVFGRD96 79.0 30 75 -75 4.32 0.5819
WVFGRD96 81.0 30 75 -75 4.32 0.5788
WVFGRD96 83.0 30 75 -75 4.32 0.5787
WVFGRD96 85.0 30 75 -75 4.32 0.5780
WVFGRD96 87.0 30 75 -75 4.32 0.5748
WVFGRD96 89.0 30 75 -75 4.32 0.5715
WVFGRD96 91.0 30 75 -75 4.32 0.5693
WVFGRD96 93.0 30 75 -70 4.31 0.5683
WVFGRD96 95.0 30 75 -70 4.32 0.5661
WVFGRD96 97.0 30 80 -75 4.33 0.5640
WVFGRD96 99.0 30 80 -75 4.33 0.5636
The best solution is
WVFGRD96 41.0 245 60 0 4.16 0.7205
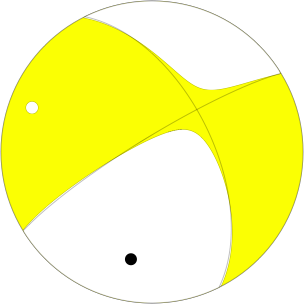
The mechanism corresponding to the best fit is
|
|
Figure 1. Waveform inversion focal mechanism
|
The best fit as a function of depth is given in the following figure:
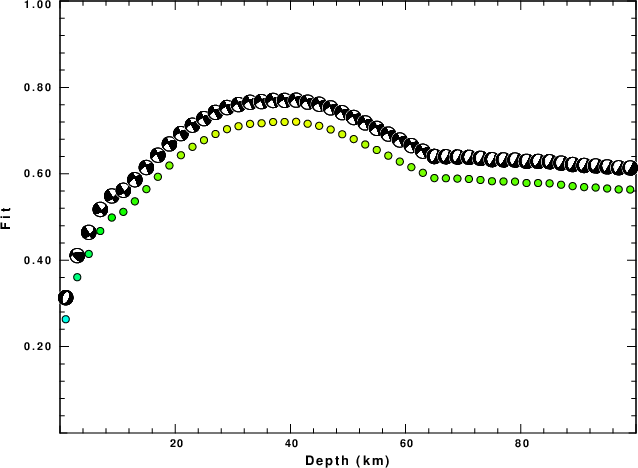
|
|
Figure 2. Depth sensitivity for waveform mechanism
|
The comparison of the observed and predicted waveforms is given in the next figure. The red traces are the observed and the blue are the predicted.
Each observed-predicted component is plotted to the same scale and peak amplitudes are indicated by the numbers to the left of each trace. A pair of numbers is given in black at the right of each predicted traces. The upper number it the time shift required for maximum correlation between the observed and predicted traces. This time shift is required because the synthetics are not computed at exactly the same distance as the observed, the velocity model used in the predictions may not be perfect and the epicentral parameters may be be off.
A positive time shift indicates that the prediction is too fast and should be delayed to match the observed trace (shift to the right in this figure). A negative value indicates that the prediction is too slow. The lower number gives the percentage of variance reduction to characterize the individual goodness of fit (100% indicates a perfect fit).
The bandpass filter used in the processing and for the display was
cut a -30 a 180
rtr
taper w 0.1
hp c 0.02 n 3
lp c 0.06 n 3
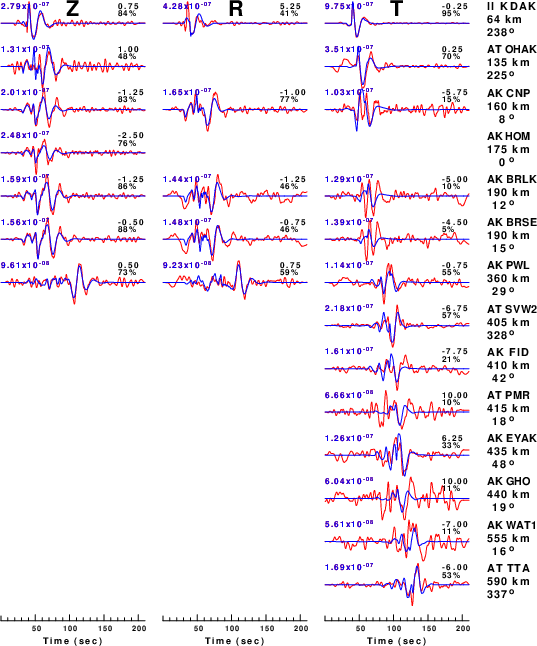
|
|
Figure 3. Waveform comparison for selected depth. Red: observed; Blue - predicted. The time shift with respect to the model prediction is indicated. The percent of fit is also indicated. The time scale is relative to the first trace sample.
|
|
|
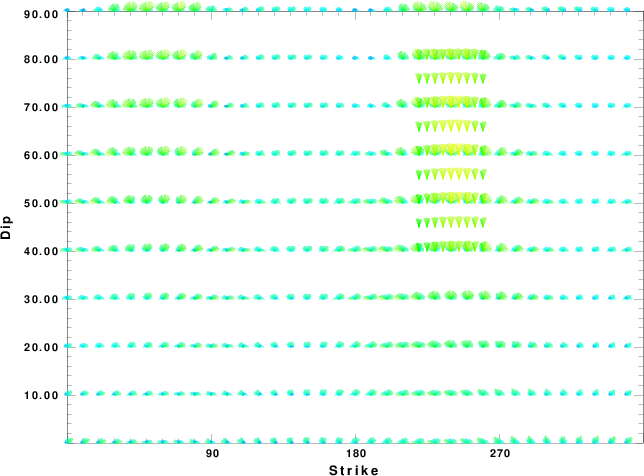
Focal mechanism sensitivity at the preferred depth. The red color indicates a very good fit to the waveforms.
Each solution is plotted as a vector at a given value of strike and dip with the angle of the vector representing the rake angle, measured, with respect to the upward vertical (N) in the figure.
|
A check on the assumed source location is possible by looking at the time shifts between the observed and predicted traces. The time shifts for waveform matching arise for several reasons:
- The origin time and epicentral distance are incorrect
- The velocity model used for the inversion is incorrect
- The velocity model used to define the P-arrival time is not the
same as the velocity model used for the waveform inversion
(assuming that the initial trace alignment is based on the
P arrival time)
Assuming only a mislocation, the time shifts are fit to a functional form:
Time_shift = A + B cos Azimuth + C Sin Azimuth
The time shifts for this inversion lead to the next figure:
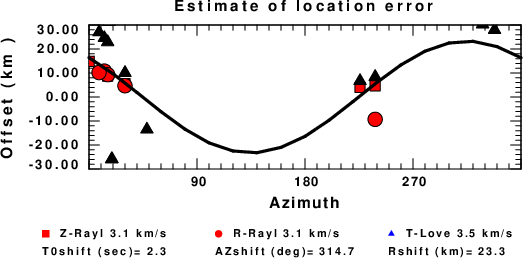
The derived shift in origin time and epicentral coordinates are given at the bottom of the figure.
Velocity Model
The WUS.model used for the waveform synthetic seismograms and for the surface wave eigenfunctions and dispersion is as follows
(The format is in the model96 format of Computer Programs in Seismology).
MODEL.01
Model after 8 iterations
ISOTROPIC
KGS
FLAT EARTH
1-D
CONSTANT VELOCITY
LINE08
LINE09
LINE10
LINE11
H(KM) VP(KM/S) VS(KM/S) RHO(GM/CC) QP QS ETAP ETAS FREFP FREFS
1.9000 3.4065 2.0089 2.2150 0.302E-02 0.679E-02 0.00 0.00 1.00 1.00
6.1000 5.5445 3.2953 2.6089 0.349E-02 0.784E-02 0.00 0.00 1.00 1.00
13.0000 6.2708 3.7396 2.7812 0.212E-02 0.476E-02 0.00 0.00 1.00 1.00
19.0000 6.4075 3.7680 2.8223 0.111E-02 0.249E-02 0.00 0.00 1.00 1.00
0.0000 7.9000 4.6200 3.2760 0.164E-10 0.370E-10 0.00 0.00 1.00 1.00
Last Changed Fri Apr 26 02:52:43 PM CDT 2024