The ANSS event ID is ld2002042000 and the event page is at https://earthquake.usgs.gov/earthquakes/eventpage/ld2002042000/executive.
2002/04/20 10:50:44 44.512 -73.697 4.8 5.3 New York
USGS/SLU Moment Tensor Solution
ENS 2002/04/20 10:50:44:0 44.51 -73.70 4.8 5.3 New York
Stations used:
CN.A54 CN.A61 CN.A64 CN.GAC CN.KGNO CN.LMQ CN.MNT CN.SADO
CN.VLDQ IU.HRV IU.SSPA LD.ACCN LD.BRNJ LD.CONY LD.CPNY
LD.MVL LD.PAL LD.SDMD PO.ELGO US.BINY US.LBNH US.NCB
Filtering commands used:
cut o DIST/3.3 -40 o DIST/3.3 +50
rtr
taper w 0.1
hp c 0.03 n 3
lp c 0.10 n 3
Best Fitting Double Couple
Mo = 2.37e+23 dyne-cm
Mw = 4.85
Z = 11 km
Plane Strike Dip Rake
NP1 187 56 97
NP2 355 35 80
Principal Axes:
Axis Value Plunge Azimuth
T 2.37e+23 78 122
N 0.00e+00 6 3
P -2.37e+23 10 272
Moment Tensor: (dyne-cm)
Component Value
Mxx 2.43e+21
Mxy 4.21e+21
Mxz -2.66e+22
Myy -2.22e+23
Myz 8.25e+22
Mzz 2.19e+23
--------#-----
----------######------
-----------##########-------
-----------#############------
------------###############-------
------------#################-------
------------###################-------
-------------###################--------
------------#####################-------
- ---------#####################--------
- P --------######### ###########-------
- --------######### T ###########-------
------------######### ###########-------
-----------######################-------
-----------######################-------
-----------####################-------
----------####################------
---------###################------
--------#################-----
--------##############------
------############----
---########---
Global CMT Convention Moment Tensor:
R T P
2.19e+23 -2.66e+22 -8.25e+22
-2.66e+22 2.43e+21 -4.21e+21
-8.25e+22 -4.21e+21 -2.22e+23
Details of the solution is found at
http://www.eas.slu.edu/eqc/eqc_mt/MECH.NA/20020420105044/index.html
|
STK = -5
DIP = 35
RAKE = 80
MW = 4.85
HS = 11.0
The NDK file is 20020420105044.ndk The waveform inversion is preferred.
The following compares this source inversion to those provided by others. The purpose is to look for major differences and also to note slight differences that might be inherent to the processing procedure. For completeness the USGS/SLU solution is repeated from above.
USGS/SLU Moment Tensor Solution
ENS 2002/04/20 10:50:44:0 44.51 -73.70 4.8 5.3 New York
Stations used:
CN.A54 CN.A61 CN.A64 CN.GAC CN.KGNO CN.LMQ CN.MNT CN.SADO
CN.VLDQ IU.HRV IU.SSPA LD.ACCN LD.BRNJ LD.CONY LD.CPNY
LD.MVL LD.PAL LD.SDMD PO.ELGO US.BINY US.LBNH US.NCB
Filtering commands used:
cut o DIST/3.3 -40 o DIST/3.3 +50
rtr
taper w 0.1
hp c 0.03 n 3
lp c 0.10 n 3
Best Fitting Double Couple
Mo = 2.37e+23 dyne-cm
Mw = 4.85
Z = 11 km
Plane Strike Dip Rake
NP1 187 56 97
NP2 355 35 80
Principal Axes:
Axis Value Plunge Azimuth
T 2.37e+23 78 122
N 0.00e+00 6 3
P -2.37e+23 10 272
Moment Tensor: (dyne-cm)
Component Value
Mxx 2.43e+21
Mxy 4.21e+21
Mxz -2.66e+22
Myy -2.22e+23
Myz 8.25e+22
Mzz 2.19e+23
--------#-----
----------######------
-----------##########-------
-----------#############------
------------###############-------
------------#################-------
------------###################-------
-------------###################--------
------------#####################-------
- ---------#####################--------
- P --------######### ###########-------
- --------######### T ###########-------
------------######### ###########-------
-----------######################-------
-----------######################-------
-----------####################-------
----------####################------
---------###################------
--------#################-----
--------##############------
------############----
---########---
Global CMT Convention Moment Tensor:
R T P
2.19e+23 -2.66e+22 -8.25e+22
-2.66e+22 2.43e+21 -4.21e+21
-8.25e+22 -4.21e+21 -2.22e+23
Details of the solution is found at
http://www.eas.slu.edu/eqc/eqc_mt/MECH.NA/20020420105044/index.html
|
REVISED Quick CMT:
04/20/2002, 10:50:44, NEW YORK, Mw=5.0
The following is a REVISED solution for the April 20, 2002,
event in New York. This CMT solution was determined by
analysis of long-period body waves (45-150 s) and
intermediate-period surface waves (40-100 s or 50-200 s).
A preliminary very-broad-band analysis of teleseismic
P waveforms gives a depth for this event of 10.4 km.
Here is the solution for the recent event.
April 20, 2002, NEW YORK, Mw=5.0
Meredith Nettles
Mike Antolik
CENTROID, MOMENT TENSOR SOLUTION
HARVARD EVENT-FILE NAME S042002A
DATA USED: GSN
L.P. BODY WAVES: 23S, 38C, T= 45
SURFACE WAVES: 27S, 58C, T= 40
CENTROID LOCATION:
ORIGIN TIME 10:50:48.2 0.2
LAT 44.69N 0.01;LON 73.80W 0.02
DEP 8.9 0.8;HALF-DURATION 1.4
MOMENT TENSOR; SCALE 10**23 D-CM
MRR= 3.19 0.17; MTT= 0.10 0.08
MFF=-3.29 0.10; MRT=-1.45 0.25
MRF=-0.46 0.18; MTF=-0.13 0.04
PRINCIPAL AXES:
1.(T) VAL= 3.78;PLG=68;AZM=172
2.(N) -0.44; 21; 6
3.(P) -3.34; 5; 274
BEST DOUBLE COUPLE:M0=3.6*10**23
NP1:STRIKE=343;DIP=44;SLIP= 59
NP2: 203; 53; 116
--#########
----------##-------
-----------###---------
-----------#######---------
-----------##########--------
-----------############--------
----------##############-------
--------###############--------
P -------#################-------
------##################-------
--------######## #######-------
-------######## T #######------
-------######## #######------
------##################-----
-----#################-----
----###############----
--##############---
###########
|
 |
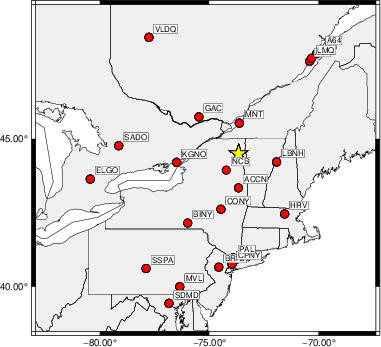
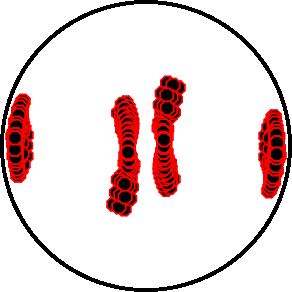
The focal mechanism was determined using broadband seismic waveforms. The location of the event (star) and the stations used for (red) the waveform inversion are shown in the next figure.
|
|
|
The program wvfgrd96 was used with good traces observed at short distance to determine the focal mechanism, depth and seismic moment. This technique requires a high quality signal and well determined velocity model for the Green's functions. To the extent that these are the quality data, this type of mechanism should be preferred over the radiation pattern technique which requires the separate step of defining the pressure and tension quadrants and the correct strike.
The observed and predicted traces are filtered using the following gsac commands:
cut o DIST/3.3 -40 o DIST/3.3 +50 rtr taper w 0.1 hp c 0.03 n 3 lp c 0.10 n 3The results of this grid search are as follow:
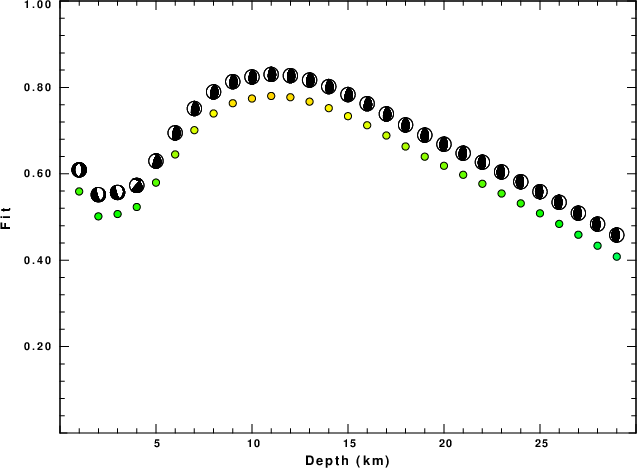
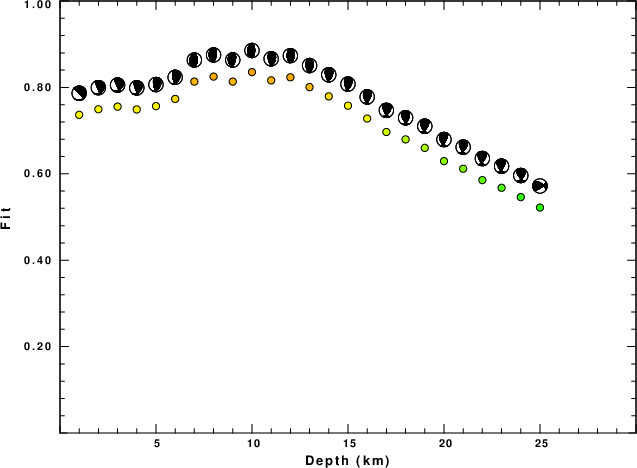
DEPTH STK DIP RAKE MW FIT
WVFGRD96 1.0 0 55 -90 4.72 0.5592
WVFGRD96 2.0 25 20 -50 4.81 0.5016
WVFGRD96 3.0 20 20 -55 4.76 0.5069
WVFGRD96 4.0 325 35 15 4.72 0.5232
WVFGRD96 5.0 345 30 60 4.78 0.5797
WVFGRD96 6.0 355 30 75 4.80 0.6449
WVFGRD96 7.0 355 35 75 4.81 0.7011
WVFGRD96 8.0 355 35 75 4.81 0.7397
WVFGRD96 9.0 355 35 80 4.82 0.7634
WVFGRD96 10.0 355 35 80 4.85 0.7743
WVFGRD96 11.0 -5 35 80 4.85 0.7802
WVFGRD96 12.0 355 35 80 4.85 0.7773
WVFGRD96 13.0 355 35 80 4.85 0.7671
WVFGRD96 14.0 350 35 75 4.85 0.7520
WVFGRD96 15.0 350 35 70 4.85 0.7335
WVFGRD96 16.0 350 35 70 4.86 0.7124
WVFGRD96 17.0 350 35 70 4.86 0.6887
WVFGRD96 18.0 355 45 80 4.86 0.6633
WVFGRD96 19.0 -5 45 80 4.87 0.6397
WVFGRD96 20.0 0 50 85 4.90 0.6186
WVFGRD96 21.0 0 50 85 4.90 0.5978
WVFGRD96 22.0 185 40 95 4.91 0.5770
WVFGRD96 23.0 185 35 95 4.91 0.5544
WVFGRD96 24.0 0 55 90 4.91 0.5316
WVFGRD96 25.0 0 55 90 4.92 0.5086
WVFGRD96 26.0 0 55 90 4.92 0.4841
WVFGRD96 27.0 185 35 95 4.93 0.4590
WVFGRD96 28.0 185 30 95 4.93 0.4336
WVFGRD96 29.0 0 60 90 4.93 0.4083
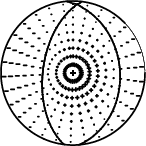
The best solution is
WVFGRD96 11.0 -5 35 80 4.85 0.7802
The mechanism corresponding to the best fit is
|
|
|
The best fit as a function of depth is given in the following figure:
|
|
|
The comparison of the observed and predicted waveforms is given in the next figure. The red traces are the observed and the blue are the predicted. Each observed-predicted component is plotted to the same scale and peak amplitudes are indicated by the numbers to the left of each trace. A pair of numbers is given in black at the right of each predicted traces. The upper number it the time shift required for maximum correlation between the observed and predicted traces. This time shift is required because the synthetics are not computed at exactly the same distance as the observed, the velocity model used in the predictions may not be perfect and the epicentral parameters may be be off. A positive time shift indicates that the prediction is too fast and should be delayed to match the observed trace (shift to the right in this figure). A negative value indicates that the prediction is too slow. The lower number gives the percentage of variance reduction to characterize the individual goodness of fit (100% indicates a perfect fit).
The bandpass filter used in the processing and for the display was
cut o DIST/3.3 -40 o DIST/3.3 +50 rtr taper w 0.1 hp c 0.03 n 3 lp c 0.10 n 3
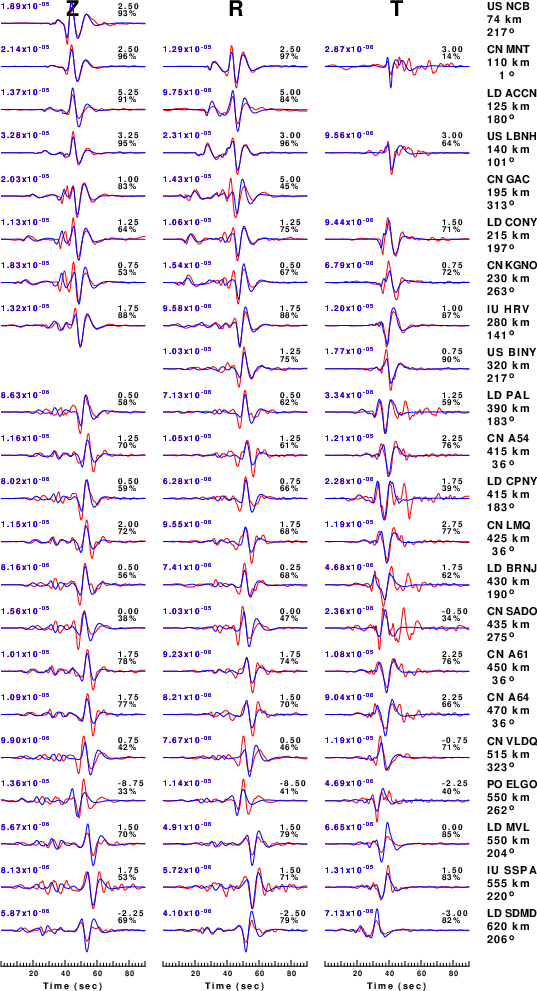
|
| Figure 3. Waveform comparison for selected depth. Red: observed; Blue - predicted. The time shift with respect to the model prediction is indicated. The percent of fit is also indicated. The time scale is relative to the first trace sample. |
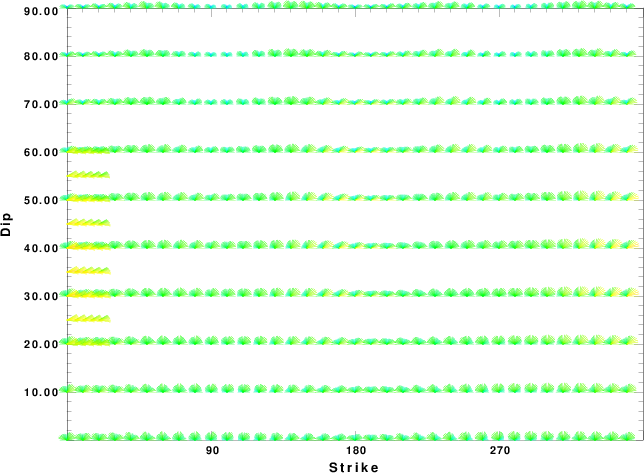
|
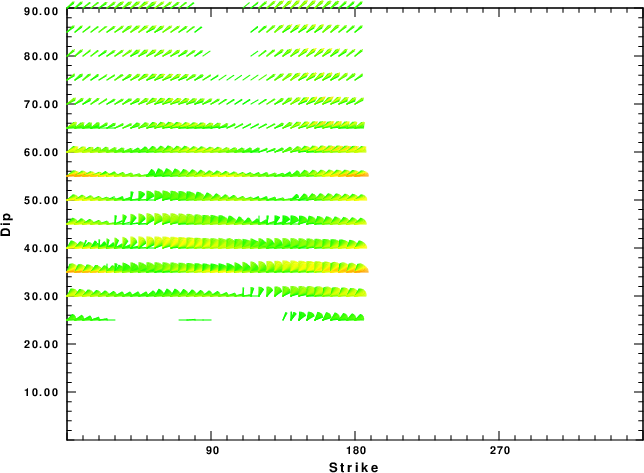
| Focal mechanism sensitivity at the preferred depth. The red color indicates a very good fit to the waveforms. Each solution is plotted as a vector at a given value of strike and dip with the angle of the vector representing the rake angle, measured, with respect to the upward vertical (N) in the figure. |
A check on the assumed source location is possible by looking at the time shifts between the observed and predicted traces. The time shifts for waveform matching arise for several reasons:
Time_shift = A + B cos Azimuth + C Sin Azimuth
The time shifts for this inversion lead to the next figure:
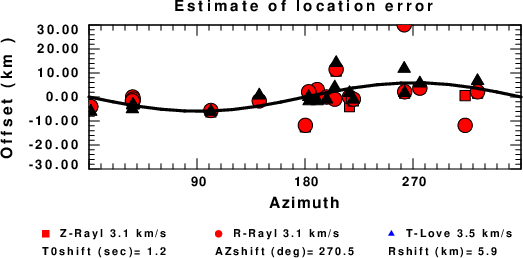
The derived shift in origin time and epicentral coordinates are given at the bottom of the figure.
The following figure shows the stations used in the grid search for the best focal mechanism to fit the surface-wave spectral amplitudes of the Love and Rayleigh waves.
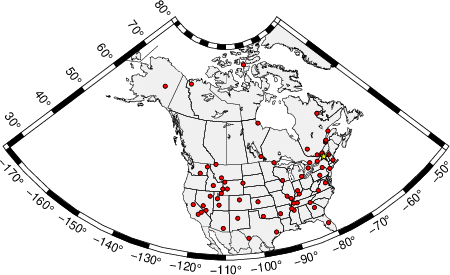
|
|
|
The surface-wave determined focal mechanism is shown here.
NODAL PLANES
STK= 179.99
DIP= 55.00
RAKE= 85.00
OR
STK= 8.66
DIP= 35.32
RAKE= 97.10
DEPTH = 10.0 km
Mw = 4.96
Best Fit 0.8355 - P-T axis plot gives solutions with FIT greater than FIT90
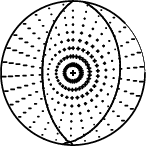 |
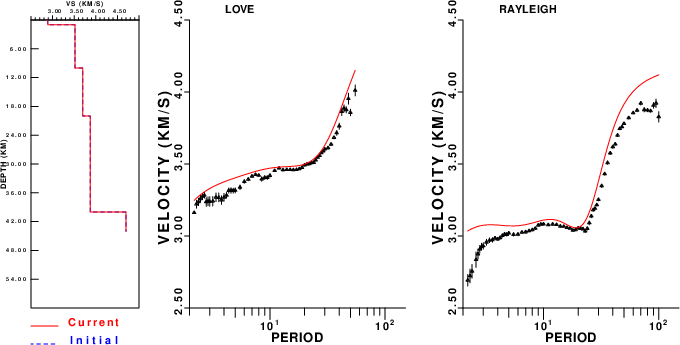
Surface wave analysis was performed using codes from Computer Programs in Seismology, specifically the multiple filter analysis program do_mft and the surface-wave radiation pattern search program srfgrd96.
Digital data were collected, instrument response removed and traces converted
to Z, R an T components. Multiple filter analysis was applied to the Z and T traces to obtain the Rayleigh- and Love-wave spectral amplitudes, respectively.
These were input to the search program which examined all depths between 1 and 25 km
and all possible mechanisms.
|
|
|
|
| Pressure-tension axis trends. Since the surface-wave spectra search does not distinguish between P and T axes and since there is a 180 ambiguity in strike, all possible P and T axes are plotted. First motion data and waveforms will be used to select the preferred mechanism. The purpose of this plot is to provide an idea of the possible range of solutions. The P and T-axes for all mechanisms with goodness of fit greater than 0.9 FITMAX (above) are plotted here. |
|
| Focal mechanism sensitivity at the preferred depth. The red color indicates a very good fit to the Love and Rayleigh wave radiation patterns. Each solution is plotted as a vector at a given value of strike and dip with the angle of the vector representing the rake angle, measured, with respect to the upward vertical (N) in the figure. Because of the symmetry of the spectral amplitude rediation patterns, only strikes from 0-180 degrees are sampled. |
|
|
The CUS.model used for the waveform synthetic seismograms and for the surface wave eigenfunctions and dispersion is as follows (The format is in the model96 format of Computer Programs in Seismology).
MODEL.01 CUS Model with Q from simple gamma values ISOTROPIC KGS FLAT EARTH 1-D CONSTANT VELOCITY LINE08 LINE09 LINE10 LINE11 H(KM) VP(KM/S) VS(KM/S) RHO(GM/CC) QP QS ETAP ETAS FREFP FREFS 1.0000 5.0000 2.8900 2.5000 0.172E-02 0.387E-02 0.00 0.00 1.00 1.00 9.0000 6.1000 3.5200 2.7300 0.160E-02 0.363E-02 0.00 0.00 1.00 1.00 10.0000 6.4000 3.7000 2.8200 0.149E-02 0.336E-02 0.00 0.00 1.00 1.00 20.0000 6.7000 3.8700 2.9020 0.000E-04 0.000E-04 0.00 0.00 1.00 1.00 0.0000 8.1500 4.7000 3.3640 0.194E-02 0.431E-02 0.00 0.00 1.00 1.00