2005/06/29 14:18:05 34.50N 129.05E 13 4.13 Korea
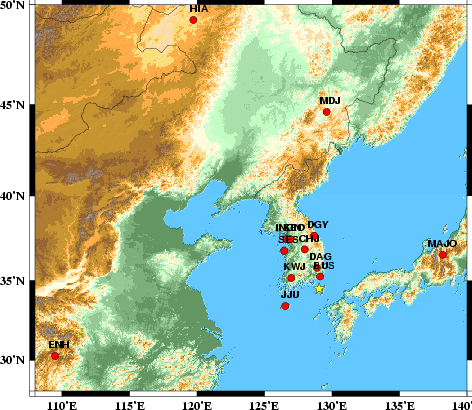
The focal mechanism was determined using broadband seismic waveforms. The location of the event and the station distribution are given in Figure 1.

|
|
|
STK = 145
DIP = 45
RAKE = 30
MW = 4.13
HS = 11
The waveform fit solution is the preferred solution. The surface wave spectral amplitude data are compatible with this solution; the surface wave data distribution was not sufficient to control the solution.
The program wvfgrd96 was used with good traces observed at short distance to determine the focal mechanism, depth and seismic moment. This technique requires a high quality signal and well determined velocity model for the Green functions. To the extent that these are the quality data, this type of mechanism should be preferred over the radiation pattern technique which requires the separate step of defining the pressure and tension quadrants and the correct strike.
The observed and predicted traces are filtered using the following gsac commands:
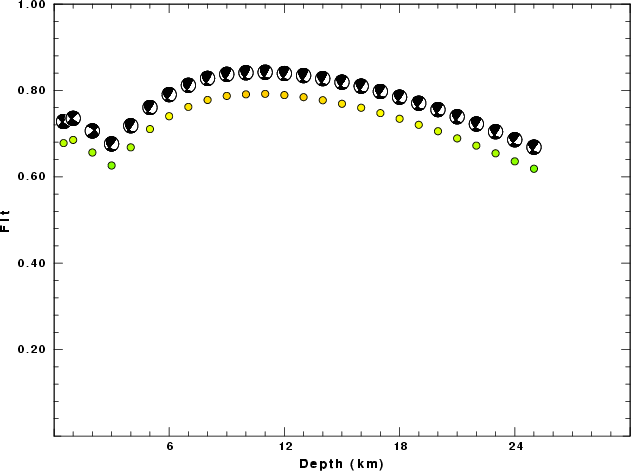
hp c 0.02 3 lp c 0.08 3 br c 0.13 0.2 n 4 p 2The results of this grid search from 0.5 to 19 km depth are as follow:
DEPTH STK DIP RAKE MW FIT
WVFGRD96 0.5 130 75 -10 3.94 0.6781
WVFGRD96 1.0 130 75 -15 3.97 0.6854
WVFGRD96 2.0 310 65 -15 4.02 0.6563
WVFGRD96 3.0 140 40 15 4.11 0.6262
WVFGRD96 4.0 140 35 20 4.13 0.6682
WVFGRD96 5.0 140 35 20 4.12 0.7105
WVFGRD96 6.0 140 35 20 4.12 0.7403
WVFGRD96 7.0 145 40 30 4.13 0.7619
WVFGRD96 8.0 145 40 30 4.13 0.7779
WVFGRD96 9.0 145 40 30 4.13 0.7873
WVFGRD96 10.0 145 40 30 4.13 0.7909
WVFGRD96 11.0 145 45 30 4.13 0.7921
WVFGRD96 12.0 145 45 30 4.14 0.7892
WVFGRD96 13.0 145 45 30 4.15 0.7844
WVFGRD96 14.0 140 45 25 4.15 0.7773
WVFGRD96 15.0 140 45 20 4.15 0.7691
WVFGRD96 16.0 140 45 20 4.16 0.7599
WVFGRD96 17.0 140 45 20 4.18 0.7475
WVFGRD96 18.0 140 45 20 4.18 0.7344
WVFGRD96 19.0 140 45 20 4.19 0.7204
WVFGRD96 20.0 140 50 20 4.20 0.7056
WVFGRD96 21.0 140 50 20 4.21 0.6890
WVFGRD96 22.0 140 50 20 4.22 0.6723
WVFGRD96 23.0 140 50 20 4.23 0.6544
WVFGRD96 24.0 135 50 10 4.23 0.6358
WVFGRD96 25.0 135 50 10 4.23 0.6187
The best solution is
WVFGRD96 11.0 145 45 30 4.13 0.7921
The mechanism correspond to the best fit is
|
|
|
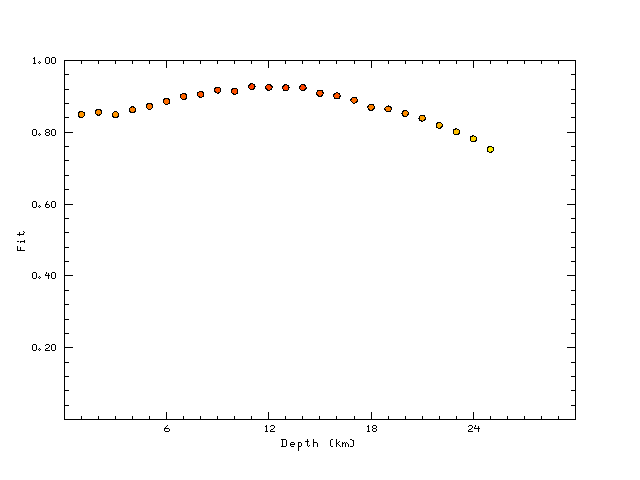
The best fit as a function of depth is given in the following figure:
|
|
|
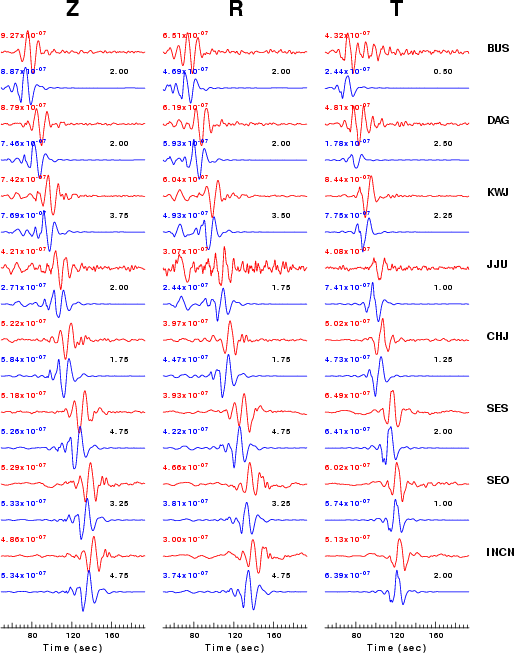
The comparison of the observed and predicted waveforms is given in the next figure. The red traces are the observed and the blue are the predicted. Each observed-predicted componnet is plotted to the same scale and peak amplitudes are indicated by the numbers to the left of each trace. The number in black at the rightr of each predicted traces it the time shift required for maximum correlation between the observed and predicted traces. This time shift is required because the synthetics are not computed at exactly the same distance as the observed and because the velocity model used in the predictions may not be perfect. A positive time shift indicates that the prediction is too fast and should be delayed to match the observed trace (shift to the right in this figure). A negative value indicates that the prediction is too slow. The bandpass filter used in the processing and for the display was
hp c 0.02 3 lp c 0.08 3 br c 0.13 0.2 n 4 p 2
|
|
|
|
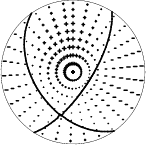
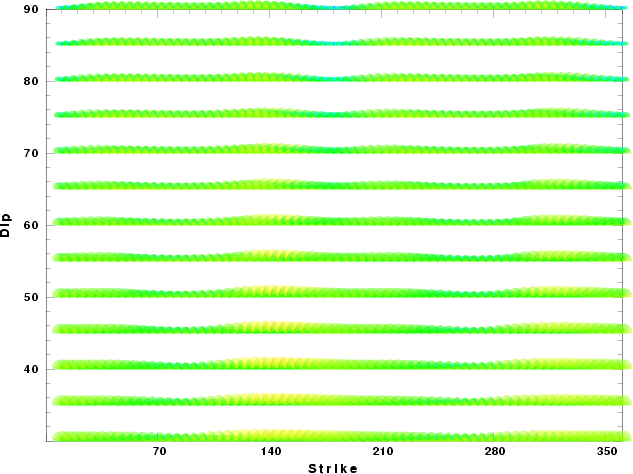
| Focal mechanism sensitivity at the preferred depth. The red color indicates a very good fit to thewavefroms. Each solution is plotted as a vector at a given value of strike and dip with the angle of the vector representing the rake angle, measured, with respect to the upward vertical (N) in the figure. |
NODAL PLANES
STK= 224.99
DIP= 70.00
RAKE= -134.99
OR
STK= 116.10
DIP= 48.36
RAKE= -27.24
DEPTH = 11.0 km
Mw = 4.14
Best Fit 0.9271 - P-T axis plot gives solutions with FIT greater than FIT90
 |
The P-wave first motion data for focal mechanism studies are as follow:
Sta Az(deg) Dist(km) First motion BUS 4 83 iP_+ DAG 354 141 eP_C KWJ 292 202 eP_X JJU 244 260 eP_X CHJ 340 281 eP_X SES 318 346 eP_+ SEO 331 383 eP_X INCN 327 396 iP_+
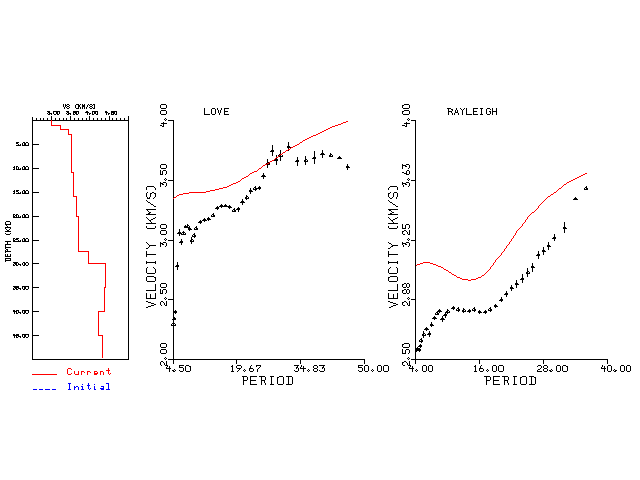
Surface wave analysis was performed using codes from Computer Programs in Seismology, specifically the multiple filter analysis program do_mft and the surface-wave radiation pattern search program srfgrd96.
Digital data were collected, instrument response removed and traces converted
to Z, R an T components. Multiple filter analysis was applied to the Z and T traces to obtain the Rayleigh- and Love-wave spectral amplitudes, respectively.
These were input to the search program which examined all depths between 1 and 25 km
and all possible mechanisms.
|
|
|

|
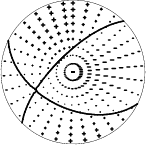
| Pressure-tension axis trends. Since the surface-wave spectra search does not distinguish between P and T axes and since there is a 180 ambiguity in strike, all possible P and T axes are plotted. First motion data and waveforms will be used to select the preferred mechanism. The purpose of this plot is to provide an idea of the possible range of solutions. The P and T-axes for all mechanisms with goodness of fit greater than 0.9 FITMAX (above) are plotted here. |
|
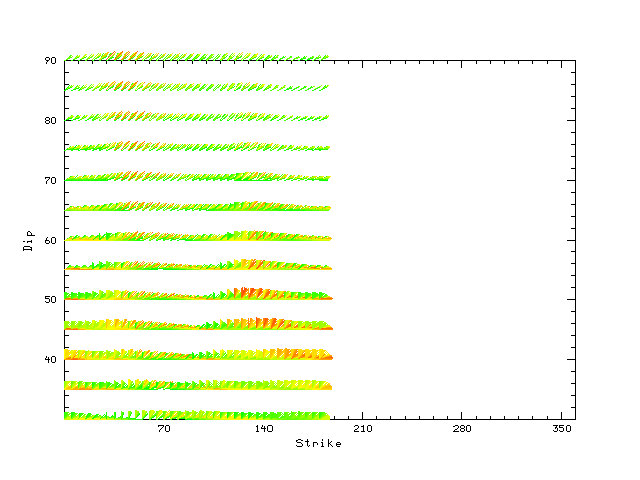
| Focal mechanism sensitivity at the preferred depth. The red color indicates a very good fit to the Love and Rayleigh wave radiation patterns. Each solution is plotted as a vector at a given value of strike and dip with the angle of the vector representing the rake angle, measured, with respect to the upward vertical (N) in the figure. Because of the symmetry of the spectral amplitude rediation patterns, only strikes from 0-180 degrees are sampled. |
The distribution of broadband stations with azimuth and distance is
Sta Az(deg) Dist(km) BUS 4 83 DAG 354 141 KWJ 292 202 JJU 244 260 CHJ 340 281 SES 318 346 DGY 355 356 SEO 330 383 INCN 327 396 MAJO 72 861 MDJ 2 1124 HIA 338 1810 ENH 261 1896
Since the analysis of the surface-wave radiation patterns uses only spectral amplitudes and because the surfave-wave radiation patterns have a 180 degree symmetry, each surface-wave solution consists of four possible focal mechanisms corresponding to the interchange of the P- and T-axes and a roation of the mechanism by 180 degrees. To select one mechanism, P-wave first motion can be used. This was not possible in this case because all the P-wave first motions were emergent ( a feature of the P-wave wave takeoff angle, the station location and the mechanism). The other way to select among the mechanisms is to compute forward synthetics and compare the observed and predicted waveforms.
The fits to the waveforms with the given mechanism are show below:
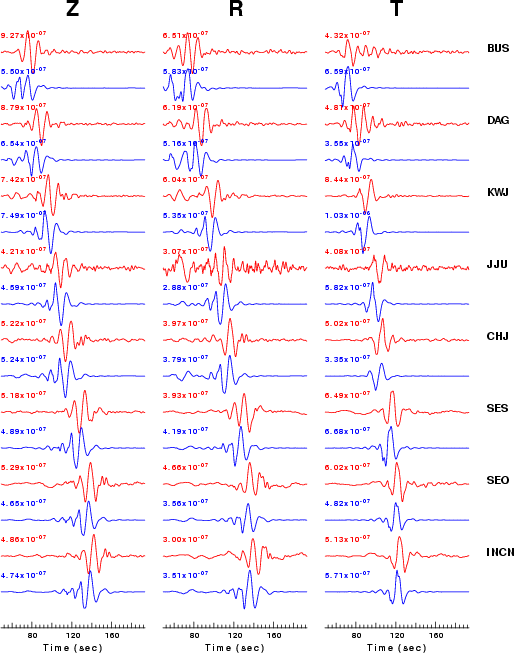
|
This figure shows the fit to the three components of motion (Z - vertical, R-radial and T - transverse). For each station and component, the observed traces is shown in red and the model predicted trace in blue. The traces represent filtered ground velocity in units of meters/sec (the peak value is printed adjacent to each trace; each pair of traces to plotted to the same scale to emphasize the difference in levels). Both synthetic and observed traces have been filtered using the SAC commands:
hp c 0.02 3 lp c 0.08 3 br c 0.13 0.2 n 4 p 2
|
|
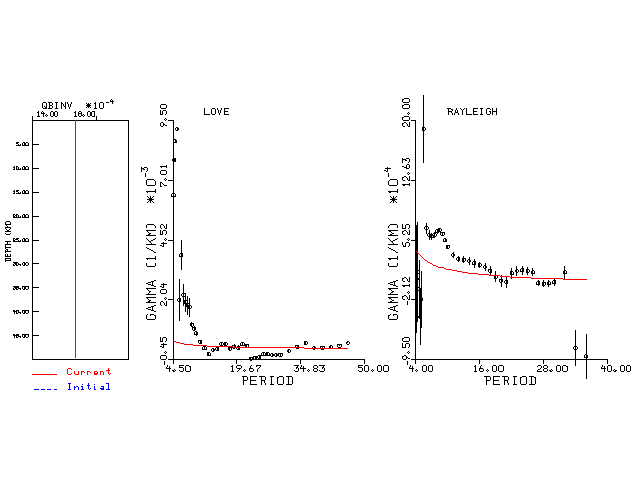
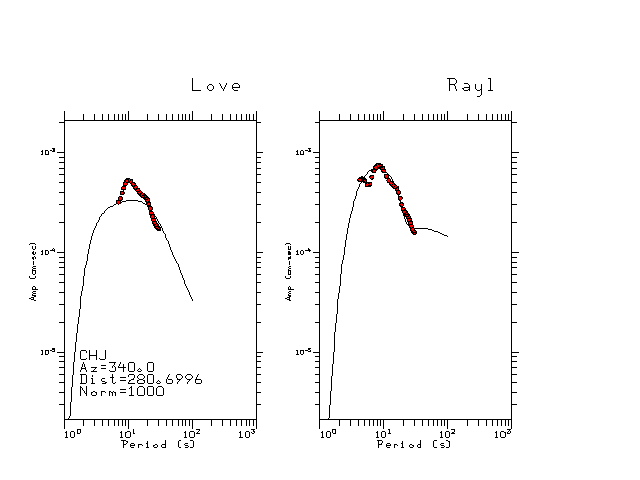
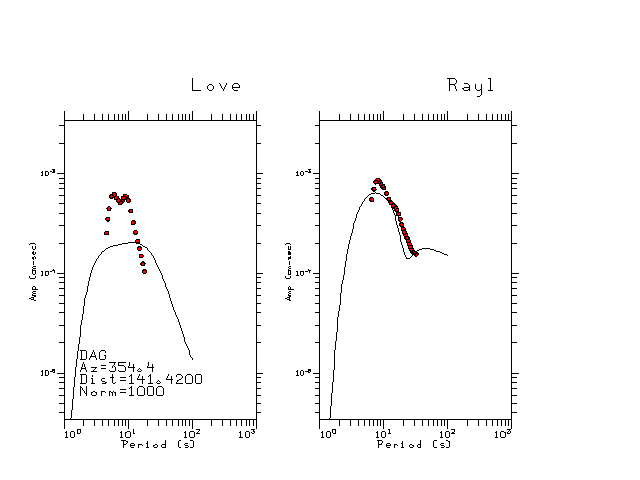
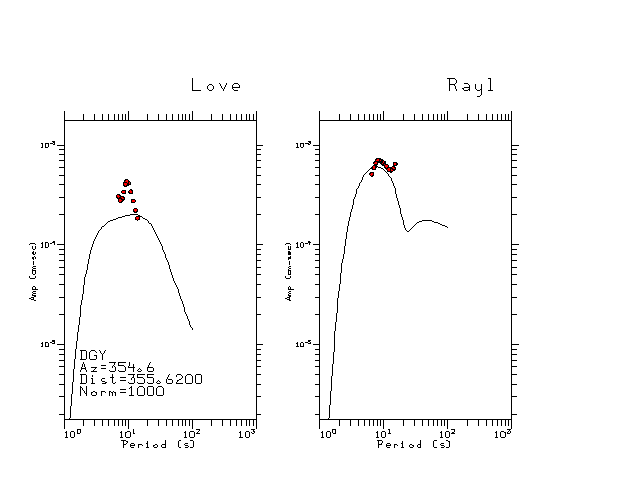
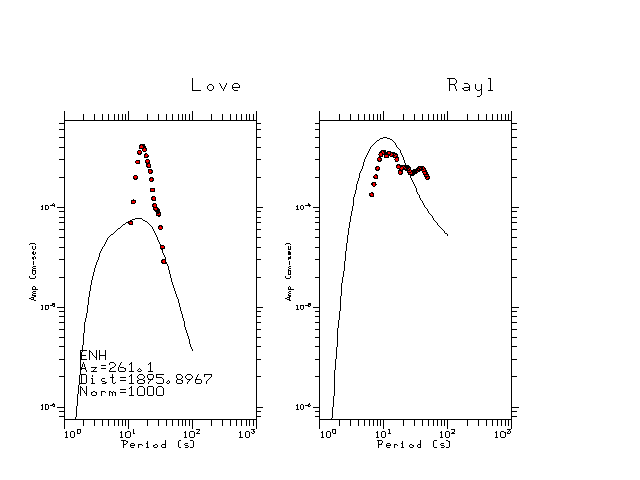
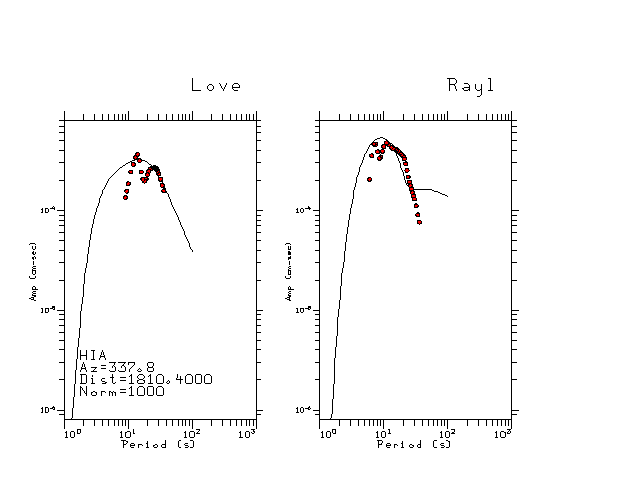
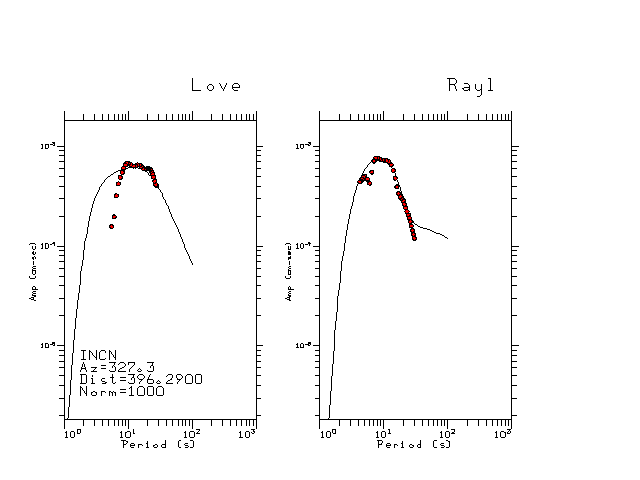
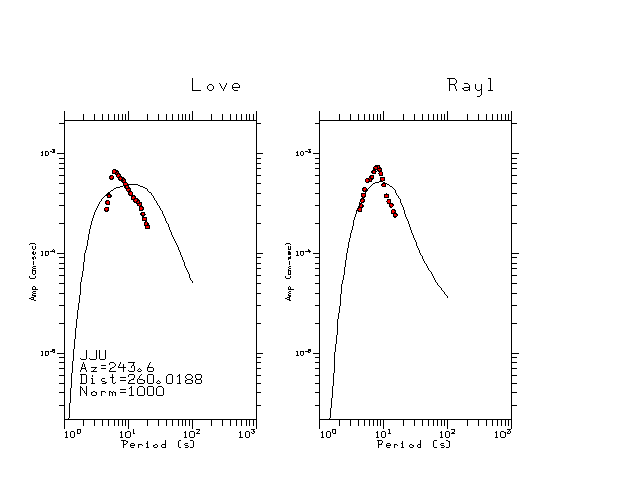
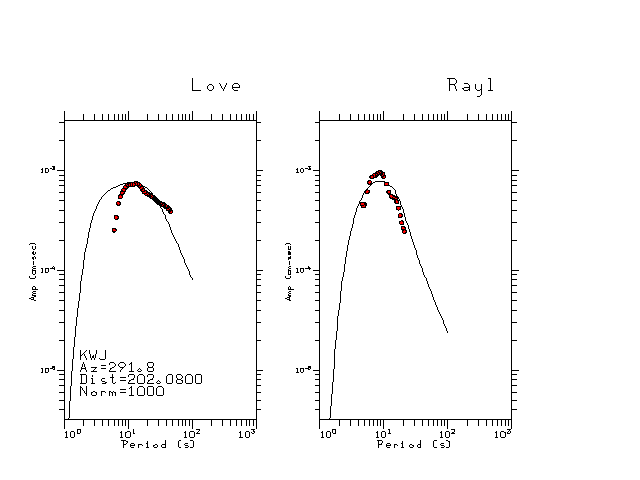
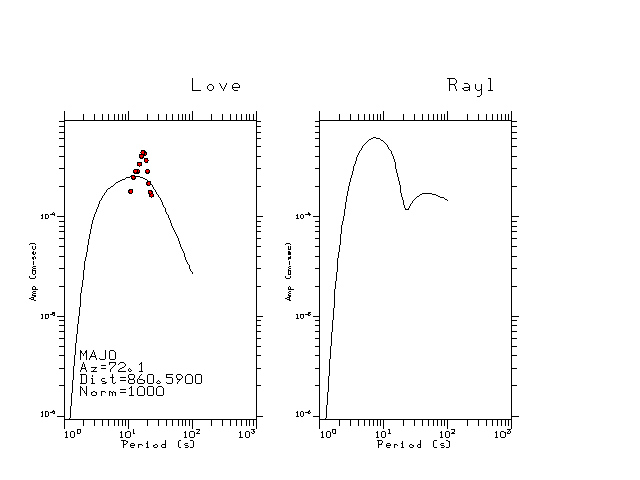
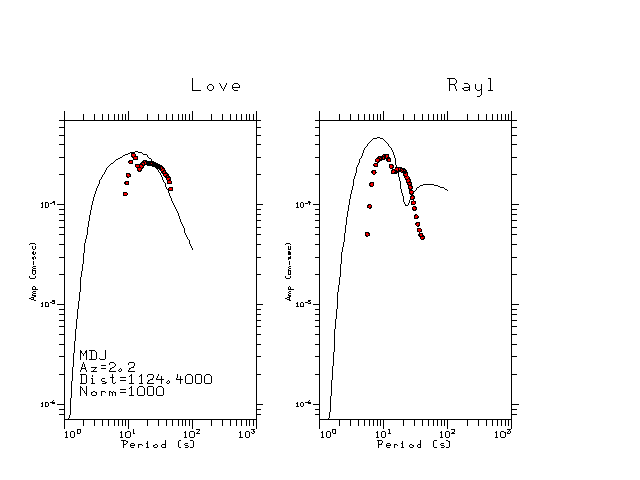
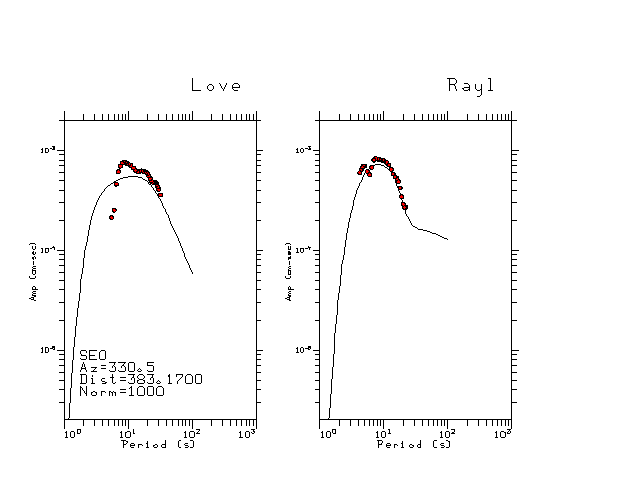
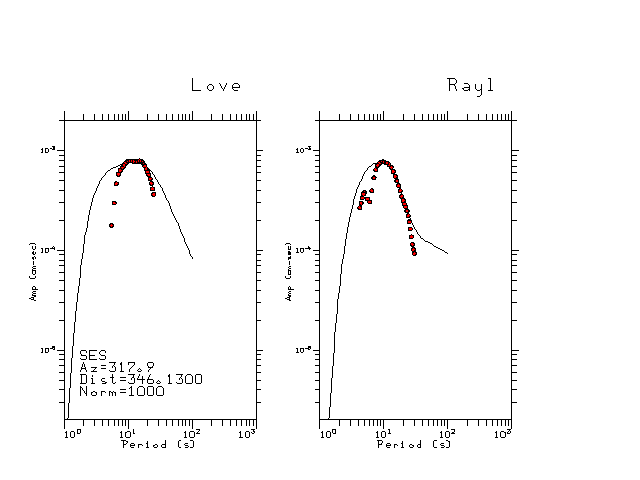
The figures below show the observed spectral amplitudes (units of cm-sec) at each station and the
theoretical predictions as a function of period for the mechanism given above. The modified Utah model earth model
was used to define the Green's functions. For each station, the Love and Rayleigh wave spectrail amplitudes are plotted with the same scaling so that one can get a sense fo the effects of the effects of the focal mechanism and depth on the excitation of each.
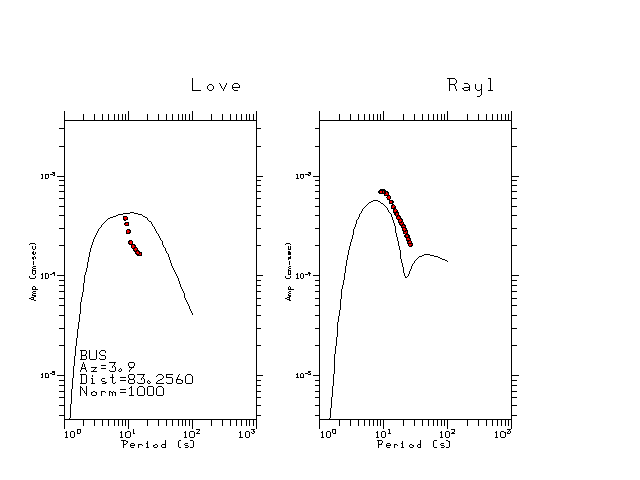 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Here we tabulate the reasons for not using certain digital data sets