2003/10/13 09:12:05 36.95N 126.51E 9 3.42 Korea
SLU Moment Tensor Solution
2003/10/13 09:12:05 36.95N 126.51E 9 3.42 Korea
Best Fitting Double Couple
Mo = 5.43e+21 dyne-cm
Mw = 3.79
Z = 11 km
Plane Strike Dip Rake
NP1 120 80 15
NP2 27 75 170
Principal Axes:
Axis Value Plunge Azimuth
T 5.43e+21 18 344
N 0.00e+00 72 153
P -5.43e+21 3 253
Moment Tensor: (dyne-cm)
Component Value
Mxx 4.11e+21
Mxy -2.79e+21
Mxz 1.60e+21
Myy -4.60e+21
Myz -1.29e+20
Mzz 4.81e+20
##############
##### #############-
######## T ############-----
######### ############------
##########################--------
##########################----------
---########################-----------
------#####################-------------
--------##################--------------
------------##############----------------
---------------###########----------------
------------------#######-----------------
---------------------###------------------
--------------------#-----------------
P -------------------######-------------
------------------###########--------
----------------###################-
--------------####################
----------####################
--------####################
---###################
##############
Harvard Convention
Moment Tensor:
R T F
4.81e+20 1.60e+21 1.29e+20
1.60e+21 4.11e+21 2.79e+21
1.29e+20 2.79e+21 -4.60e+21
|
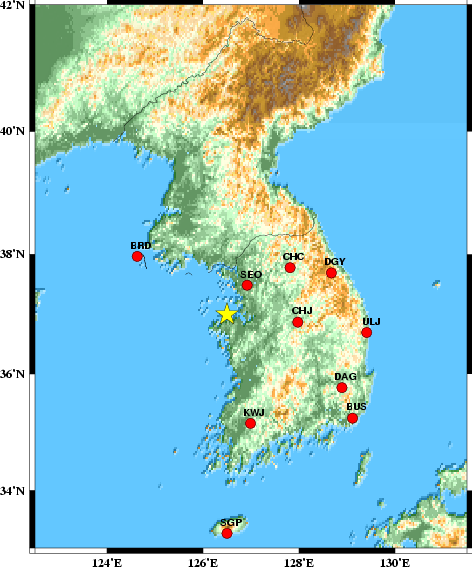
The focal mechanism was determined using broadband seismic waveforms. The location of the event and the station distribution are given in Figure 1.

|
|
|
STK = 120
DIP = 80
RAKE = 15
MW = 3.79
HS = 11
The waveform inversion is preferred. This solution agrees with the surface-wave solution. This solution is well determined.
The program wvfgrd96 was used with good traces observed at short distance to determine the focal mechanism, depth and seismic moment. This technique requires a high quality signal and well determined velocity model for the Green functions. To the extent that these are the quality data, this type of mechanism should be preferred over the radiation pattern technique which requires the separate step of defining the pressure and tension quadrants and the correct strike.
The observed and predicted traces are filtered using the following gsac commands:
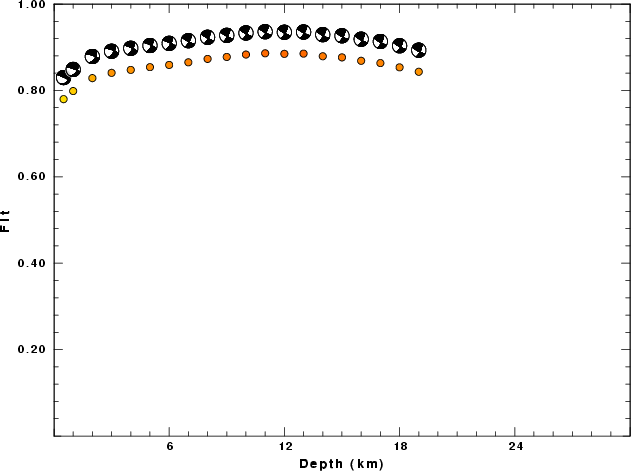
hp c 0.02 3 lp c 0.10 3 br c 0.2 0.5 n 4 p 2The results of this grid search from 0.5 to 19 km depth are as follow:
DEPTH STK DIP RAKE MW FIT
WVFGRD96 0.5 295 85 -65 3.87 0.7798
WVFGRD96 1.0 290 80 -50 3.78 0.7986
WVFGRD96 2.0 290 75 -40 3.74 0.8285
WVFGRD96 3.0 290 70 -30 3.75 0.8407
WVFGRD96 4.0 295 80 -25 3.73 0.8475
WVFGRD96 5.0 295 80 -20 3.74 0.8539
WVFGRD96 6.0 295 80 -20 3.74 0.8590
WVFGRD96 7.0 120 80 15 3.75 0.8651
WVFGRD96 8.0 120 80 15 3.76 0.8730
WVFGRD96 9.0 120 80 15 3.77 0.8775
WVFGRD96 10.0 120 80 15 3.77 0.8831
WVFGRD96 11.0 120 80 15 3.79 0.8859
WVFGRD96 12.0 120 80 15 3.80 0.8847
WVFGRD96 13.0 120 80 15 3.81 0.8852
WVFGRD96 14.0 120 80 15 3.83 0.8791
WVFGRD96 15.0 120 80 20 3.82 0.8765
WVFGRD96 16.0 120 80 20 3.83 0.8686
WVFGRD96 17.0 120 80 20 3.85 0.8633
WVFGRD96 18.0 120 80 20 3.87 0.8534
WVFGRD96 19.0 120 75 25 3.87 0.8432
The best solution is
WVFGRD96 11.0 120 80 15 3.79 0.8859
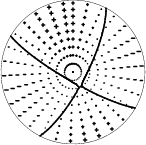
The mechanism correspond to the best fit is
|
|
|
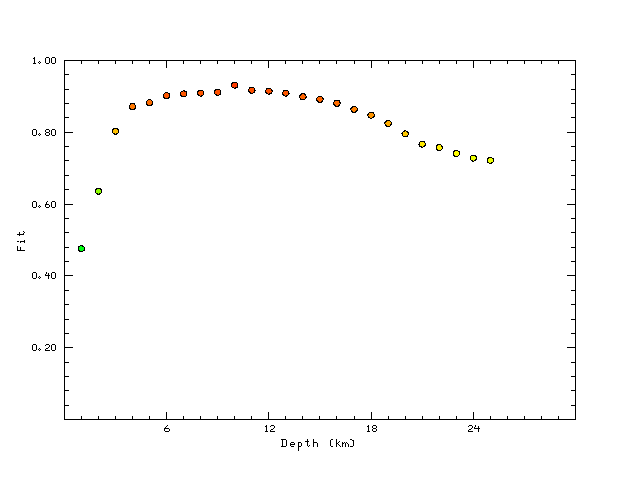
The best fit as a function of depth is given in the following figure:
|
|
|
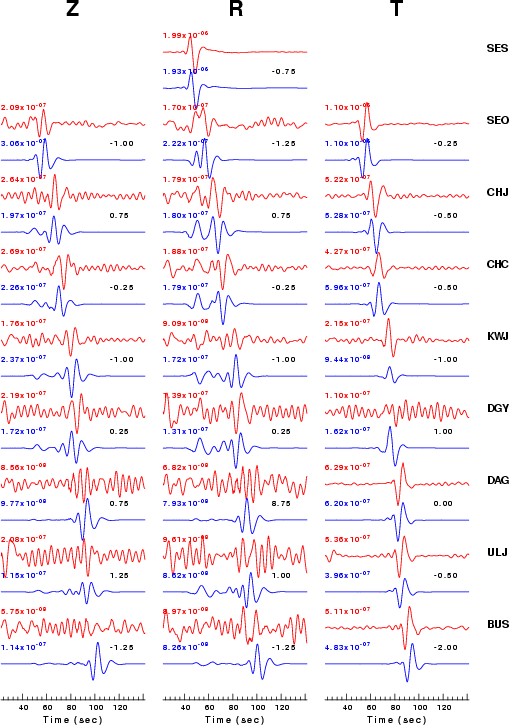
The comparison of the observed and predicted waveforms is given in the next figure. The red traces are the observed and the blue are the predicted. Each observed-predicted componnet is plotted to the same scale and peak amplitudes are indicated by the numbers to the left of each trace. The number in black at the rightr of each predicted traces it the time shift required for maximum correlation between the observed and predicted traces. This time shift is required because the synthetics are not computed at exactly the same distance as the observed and because the velocity model used in the predictions may not be perfect. A positive time shift indicates that the prediction is too fast and should be delayed to match the observed trace (shift to the right in this figure). A negative value indicates that the prediction is too slow. The bandpass filter used in the processing and for the display was
hp c 0.02 3 lp c 0.10 3 br c 0.2 0.5 n 4 p 2
|
|
|
|
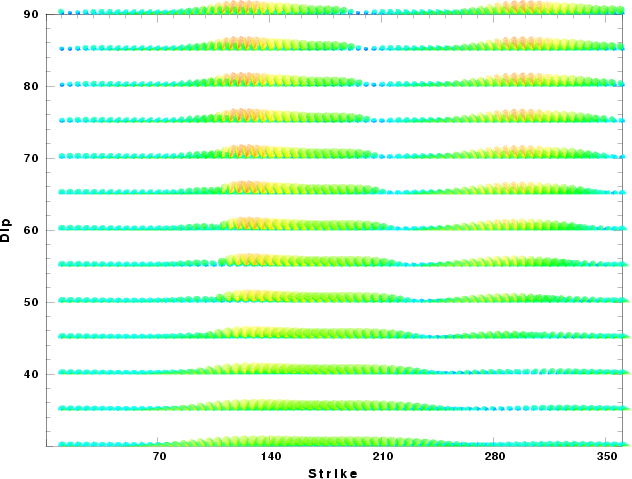
| Focal mechanism sensitivity at the preferred depth. The red color indicates a very good fit to thewavefroms. Each solution is plotted as a vector at a given value of strike and dip with the angle of the vector representing the rake angle, measured, with respect to the upward vertical (N) in the figure. |
NODAL PLANES
STK= 293.24
DIP= 80.14
RAKE= -10.15
OR
STK= 25.00
DIP= 80.00
RAKE= -169.99
DEPTH = 10.0 km
Mw = 3.79
Best Fit 0.9310 - P-T axis plot gives solutions with FIT greater than FIT90
 |
The P-wave first motion data for focal mechanism studies are as follow:
Sta Az(deg) Dist(km) First motion SEO 31 70 iP_D CHJ 93 131 eP_- CHC 51 148 eP_X KWJ 168 203 eP_+ DGY 66 209 eP_X DAG 121 251 eP_X ULJ 95 260 eP_X BUS 128 301 eP_X
Surface wave analysis was performed using codes from Computer Programs in Seismology, specifically the multiple filter analysis program do_mft and the surface-wave radiation pattern search program srfgrd96.
Digital data were collected, instrument response removed and traces converted
to Z, R an T components. Multiple filter analysis was applied to the Z and T traces to obtain the Rayleigh- and Love-wave spectral amplitudes, respectively.
These were input to the search program which examined all depths between 1 and 25 km
and all possible mechanisms.
|
|
|
|
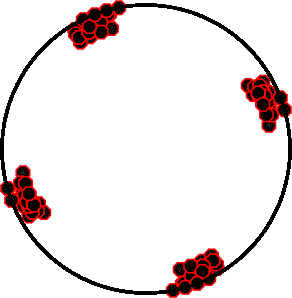
| Pressure-tension axis trends. Since the surface-wave spectra search does not distinguish between P and T axes and since there is a 180 ambiguity in strike, all possible P and T axes are plotted. First motion data and waveforms will be used to select the preferred mechanism. The purpose of this plot is to provide an idea of the possible range of solutions. The P and T-axes for all mechanisms with goodness of fit greater than 0.9 FITMAX (above) are plotted here. |
|
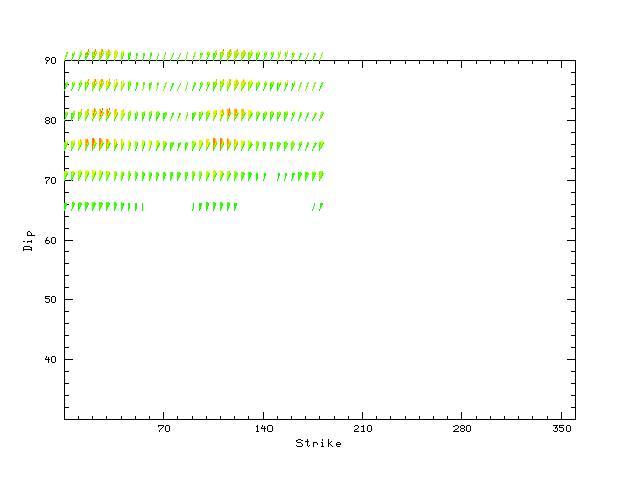
| Focal mechanism sensitivity at the preferred depth. The red color indicates a very good fit to the Love and Rayleigh wave radiation patterns. Each solution is plotted as a vector at a given value of strike and dip with the angle of the vector representing the rake angle, measured, with respect to the upward vertical (N) in the figure. Because of the symmetry of the spectral amplitude rediation patterns, only strikes from 0-180 degrees are sampled. |
The distribution of broadband stations with azimuth and distance is
Sta Az(deg) Dist(km) SEO 34 66 CHJ 96 132 CHC 53 145 BRD 304 197 DGY 68 207 KWJ 168 209 DAG 122 255 ULJ 96 261 BUS 129 305 SGP 180 415
Since the analysis of the surface-wave radiation patterns uses only spectral amplitudes and because the surfave-wave radiation patterns have a 180 degree symmetry, each surface-wave solution consists of four possible focal mechanisms corresponding to the interchange of the P- and T-axes and a roation of the mechanism by 180 degrees. To select one mechanism, P-wave first motion can be used. This was not possible in this case because all the P-wave first motions were emergent ( a feature of the P-wave wave takeoff angle, the station location and the mechanism). The other way to select among the mechanisms is to compute forward synthetics and compare the observed and predicted waveforms.
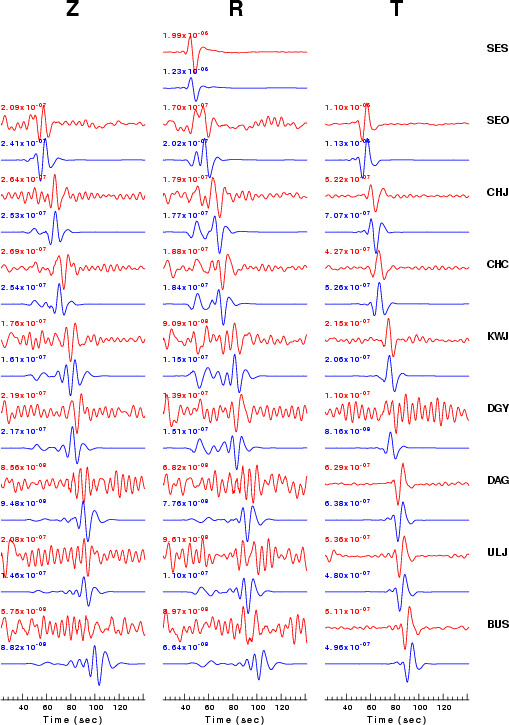
The fits to the waveforms with the given mechanism are show below:
|
This figure shows the fit to the three components of motion (Z - vertical, R-radial and T - transverse). For each station and component, the observed traces is shown in red and the model predicted trace in blue. The traces represent filtered ground velocity in units of meters/sec (the peak value is printed adjacent to each trace; each pair of traces to plotted to the same scale to emphasize the difference in levels). Both synthetic and observed traces have been filtered using the SAC commands:
hp c 0.02 3 lp c 0.10 3 br c 0.2 0.5 n 4 p 2
|
|
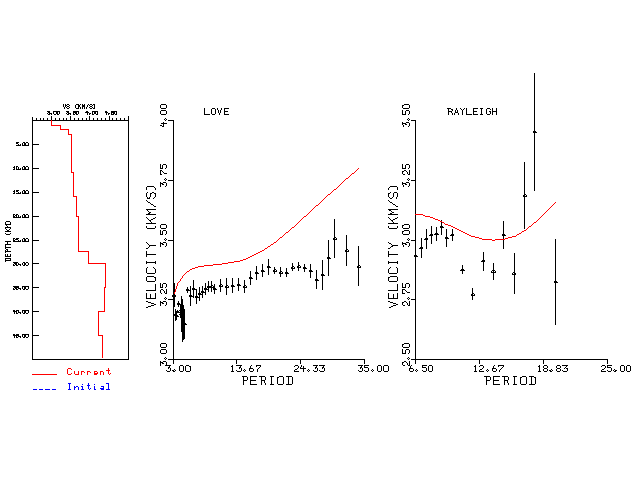
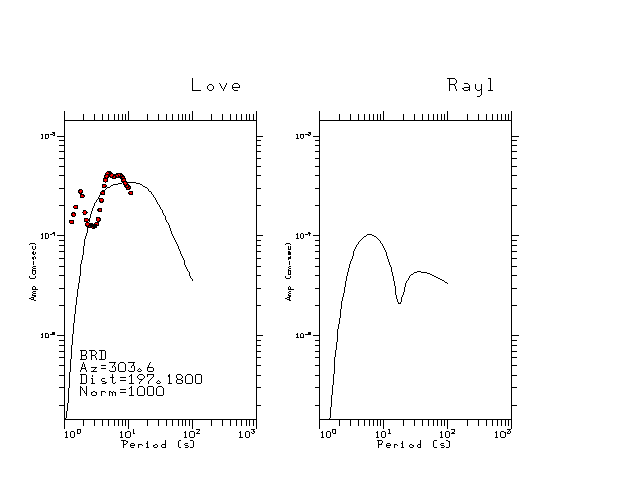
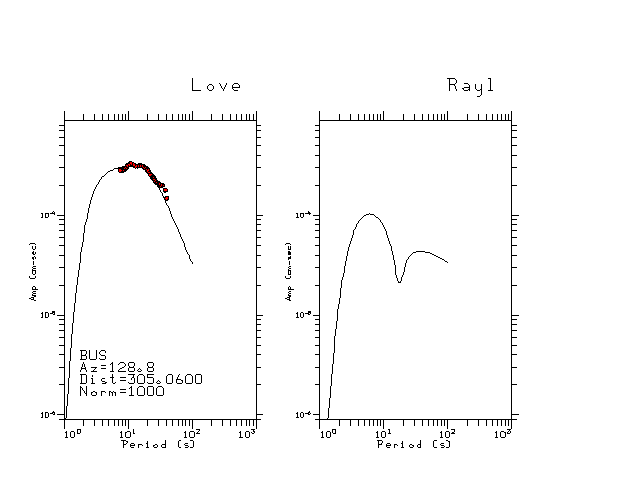
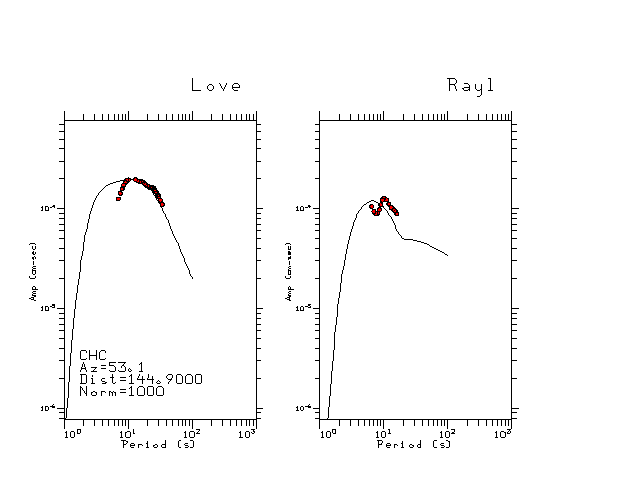
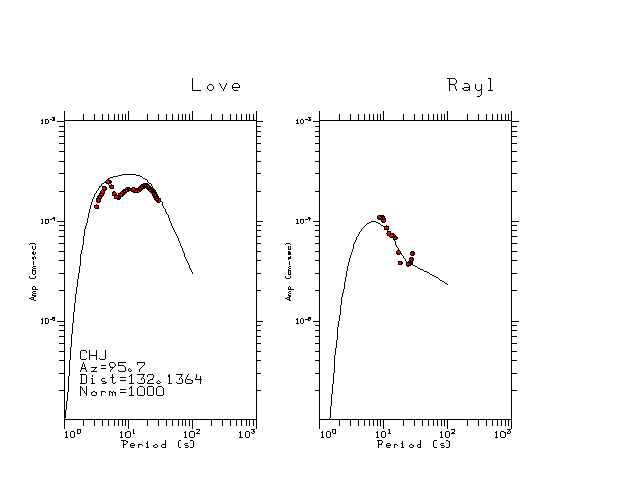
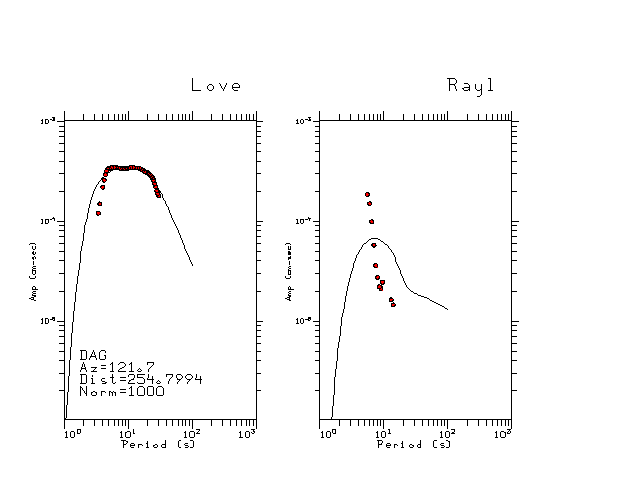
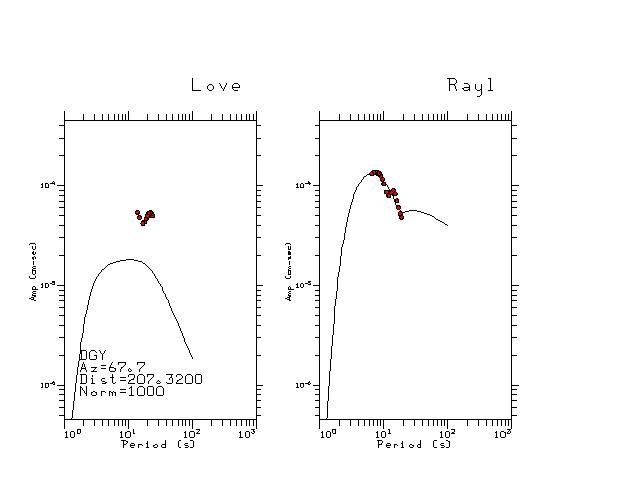
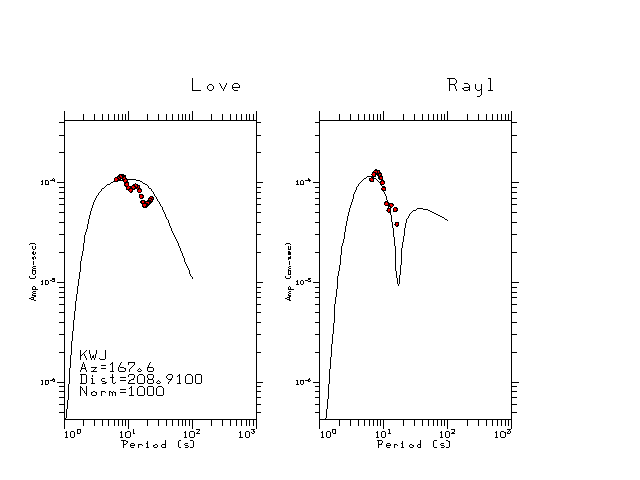
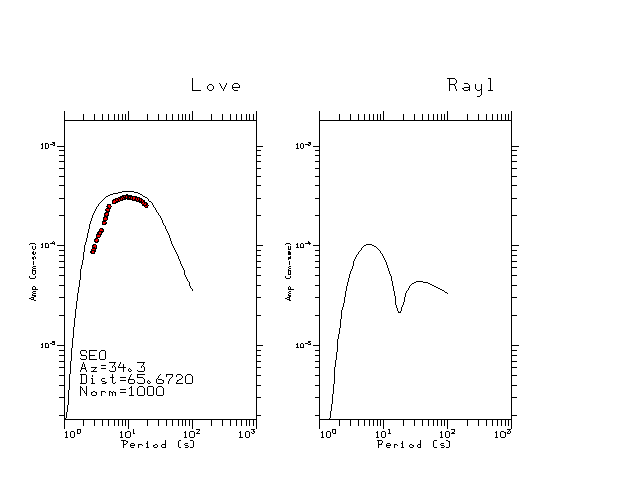
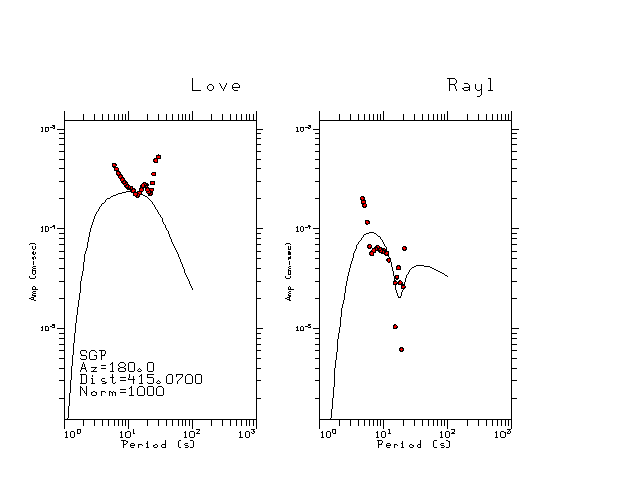
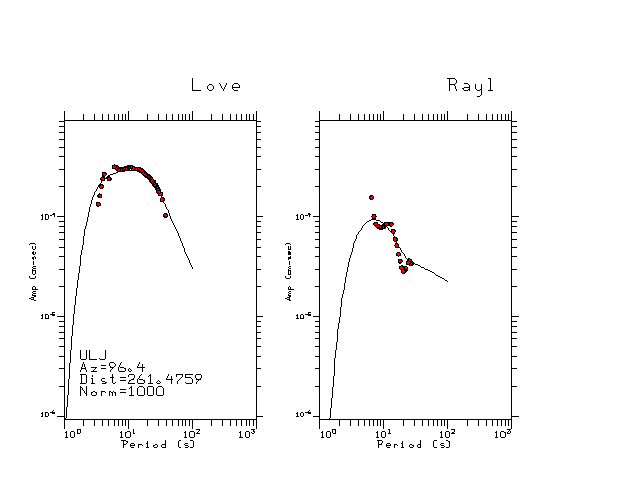
The figures below show the observed spectral amplitudes (units of cm-sec) at each station and the
theoretical predictions as a function of period for the mechanism given above. The modified Utah model earth model
was used to define the Green's functions. For each station, the Love and Rayleigh wave spectrail amplitudes are plotted with the same scaling so that one can get a sense fo the effects of the effects of the focal mechanism and depth on the excitation of each.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Here we tabulate the reasons for not using certain digital data sets