2009/04/14 07:36:44 42.495 13.395 8.8 2.9 Italy
USGS Felt map for this earthquake
USGS/SLU Moment Tensor Solution
ENS 2009/04/14 07:36:44:5 42.49 13.40 8.8 2.9 Italy
Stations used:
IV.ASSB IV.NRCA IV.TERO MN.AQU
Filtering commands used:
hp c 0.02 n 3
lp c 0.10 n 3
Best Fitting Double Couple
Mo = 3.98e+20 dyne-cm
Mw = 3.00
Z = 6 km
Plane Strike Dip Rake
NP1 108 66 -123
NP2 345 40 -40
Principal Axes:
Axis Value Plunge Azimuth
T 3.98e+20 14 221
N 0.00e+00 29 123
P -3.98e+20 56 334
Moment Tensor: (dyne-cm)
Component Value
Mxx 1.15e+20
Mxy 2.33e+20
Mxz -2.37e+20
Myy 1.37e+20
Myz 1.75e+19
Mzz -2.52e+20
----##########
-------------#########
------------------##########
---------------------#########
-------------------------#########
------------- -----------#########
-------------- P ------------#########
--------------- -------------#########
#-------------------------------########
####-----------------------------#########
######---------------------------#########
#########-------------------------########
############----------------------########
###############------------------#######
####################-------------######-
###############################-------
##############################------
#### #####################------
## T ####################-----
# ###################-----
###################---
#############-
Global CMT Convention Moment Tensor:
R T P
-2.52e+20 -2.37e+20 -1.75e+19
-2.37e+20 1.15e+20 -2.33e+20
-1.75e+19 -2.33e+20 1.37e+20
Details of the solution is found at
http://www.eas.slu.edu/eqc/eqc_mt/MECH.IT/20090414073644/index.html
|
STK = 345
DIP = 40
RAKE = -40
MW = 3.00
HS = 6.0
The waveform inversion is preferred.
The following compares this source inversion to others
USGS/SLU Moment Tensor Solution
ENS 2009/04/14 07:36:44:5 42.49 13.40 8.8 2.9 Italy
Stations used:
IV.ASSB IV.NRCA IV.TERO MN.AQU
Filtering commands used:
hp c 0.02 n 3
lp c 0.10 n 3
Best Fitting Double Couple
Mo = 3.98e+20 dyne-cm
Mw = 3.00
Z = 6 km
Plane Strike Dip Rake
NP1 108 66 -123
NP2 345 40 -40
Principal Axes:
Axis Value Plunge Azimuth
T 3.98e+20 14 221
N 0.00e+00 29 123
P -3.98e+20 56 334
Moment Tensor: (dyne-cm)
Component Value
Mxx 1.15e+20
Mxy 2.33e+20
Mxz -2.37e+20
Myy 1.37e+20
Myz 1.75e+19
Mzz -2.52e+20
----##########
-------------#########
------------------##########
---------------------#########
-------------------------#########
------------- -----------#########
-------------- P ------------#########
--------------- -------------#########
#-------------------------------########
####-----------------------------#########
######---------------------------#########
#########-------------------------########
############----------------------########
###############------------------#######
####################-------------######-
###############################-------
##############################------
#### #####################------
## T ####################-----
# ###################-----
###################---
#############-
Global CMT Convention Moment Tensor:
R T P
-2.52e+20 -2.37e+20 -1.75e+19
-2.37e+20 1.15e+20 -2.33e+20
-1.75e+19 -2.33e+20 1.37e+20
Details of the solution is found at
http://www.eas.slu.edu/eqc/eqc_mt/MECH.IT/20090414073644/index.html
|
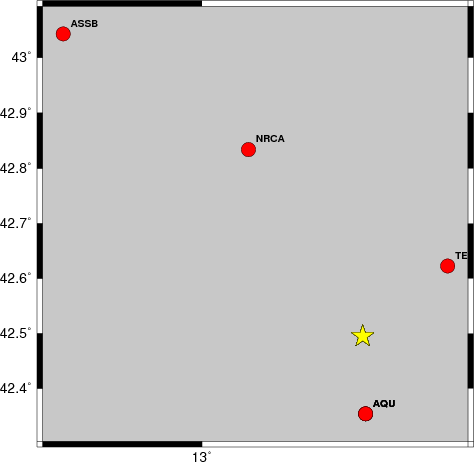
The focal mechanism was determined using broadband seismic waveforms. The location of the event and the and stations used for the waveform inversion are shown in the next figure.

|
|
|
The program wvfgrd96 was used with good traces observed at short distance to determine the focal mechanism, depth and seismic moment. This technique requires a high quality signal and well determined velocity model for the Green functions. To the extent that these are the quality data, this type of mechanism should be preferred over the radiation pattern technique which requires the separate step of defining the pressure and tension quadrants and the correct strike.
The observed and predicted traces are filtered using the following gsac commands:
hp c 0.02 n 3 lp c 0.10 n 3The results of this grid search from 0.5 to 19 km depth are as follow:
DEPTH STK DIP RAKE MW FIT
WVFGRD96 1.0 210 90 55 2.82 0.3728
WVFGRD96 2.0 350 20 -10 2.91 0.4560
WVFGRD96 3.0 350 30 -15 2.88 0.5566
WVFGRD96 4.0 350 40 -30 2.89 0.6037
WVFGRD96 5.0 350 35 -25 2.97 0.6199
WVFGRD96 6.0 345 40 -40 3.00 0.6260
WVFGRD96 7.0 350 40 -15 2.96 0.6033
WVFGRD96 8.0 350 50 -15 2.95 0.5837
WVFGRD96 9.0 350 50 -10 2.95 0.5694
WVFGRD96 10.0 345 45 -5 2.95 0.5550
WVFGRD96 11.0 345 50 -5 2.98 0.5414
WVFGRD96 12.0 340 45 -10 2.97 0.5298
WVFGRD96 13.0 340 50 -5 3.01 0.5204
WVFGRD96 14.0 335 50 -10 3.02 0.5154
WVFGRD96 15.0 330 50 -15 3.07 0.5151
WVFGRD96 16.0 325 50 -15 3.10 0.5161
WVFGRD96 17.0 325 55 -10 3.15 0.5178
WVFGRD96 18.0 325 55 -15 3.15 0.5206
WVFGRD96 19.0 325 55 -15 3.16 0.5180
WVFGRD96 20.0 320 55 -15 3.19 0.5175
WVFGRD96 21.0 220 80 25 3.21 0.5166
WVFGRD96 22.0 220 80 20 3.25 0.5242
WVFGRD96 23.0 220 80 20 3.26 0.5328
WVFGRD96 24.0 220 80 20 3.27 0.5423
WVFGRD96 25.0 215 85 20 3.26 0.5492
WVFGRD96 26.0 220 85 20 3.29 0.5567
WVFGRD96 27.0 220 85 20 3.30 0.5624
WVFGRD96 28.0 220 85 20 3.32 0.5652
WVFGRD96 29.0 35 90 -15 3.35 0.5657
The best solution is
WVFGRD96 6.0 345 40 -40 3.00 0.6260
The mechanism correspond to the best fit is
|
|
|
The best fit as a function of depth is given in the following figure:
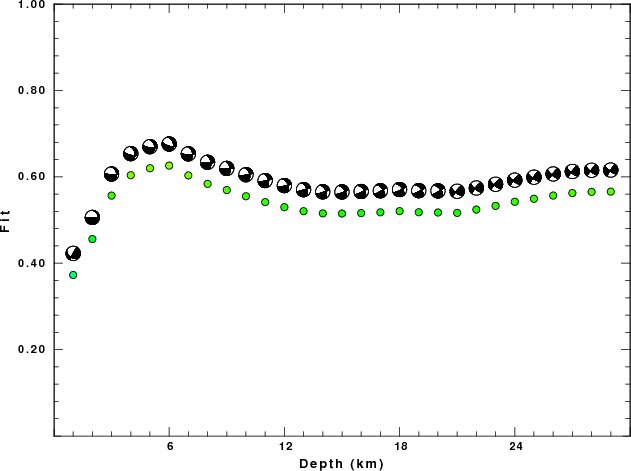
|
|
|
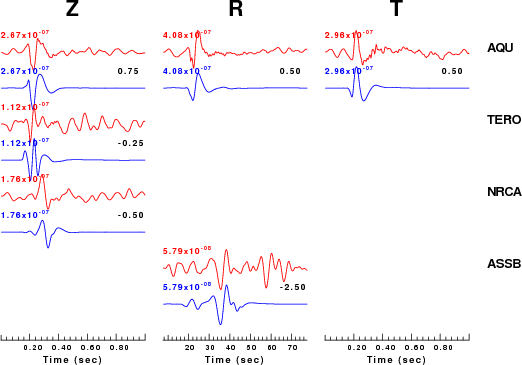
The comparison of the observed and predicted waveforms is given in the next figure. The red traces are the observed and the blue are the predicted. Each observed-predicted component is plotted to the same scale and peak amplitudes are indicated by the numbers to the left of each trace. The number in black at the rightr of each predicted traces it the time shift required for maximum correlation between the observed and predicted traces. This time shift is required because the synthetics are not computed at exactly the same distance as the observed and because the velocity model used in the predictions may not be perfect. A positive time shift indicates that the prediction is too fast and should be delayed to match the observed trace (shift to the right in this figure). A negative value indicates that the prediction is too slow. The bandpass filter used in the processing and for the display was
hp c 0.02 n 3 lp c 0.10 n 3
|
|
|
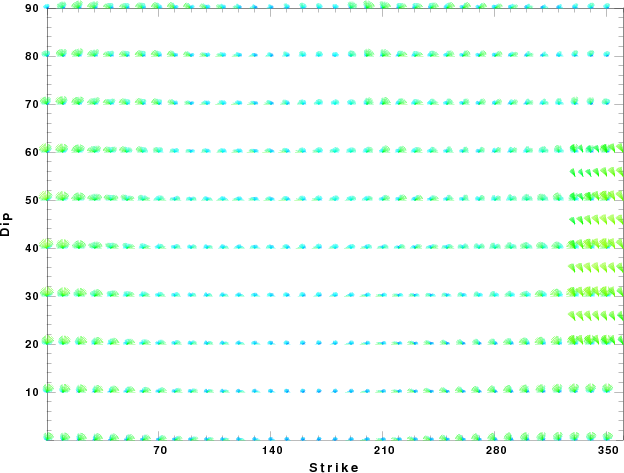
|
| Focal mechanism sensitivity at the preferred depth. The red color indicates a very good fit to thewavefroms. Each solution is plotted as a vector at a given value of strike and dip with the angle of the vector representing the rake angle, measured, with respect to the upward vertical (N) in the figure. |
The nnCIA used for the waveform synthetic seismograms and for the surface wave eigenfunctions and dispersion is as follows:
MODEL.01
C.It. A. Di Luzio et al Earth Plan Lettrs 280 (2009) 1-12 Fig 5. 7-8 MODEL/SURF3
ISOTROPIC
KGS
FLAT EARTH
1-D
CONSTANT VELOCITY
LINE08
LINE09
LINE10
LINE11
H(KM) VP(KM/S) VS(KM/S) RHO(GM/CC) QP QS ETAP ETAS FREFP FREFS
1.5000 3.7497 2.1436 2.2753 0.500E-02 0.100E-01 0.00 0.00 1.00 1.00
3.0000 4.9399 2.8210 2.4858 0.500E-02 0.100E-01 0.00 0.00 1.00 1.00
3.0000 6.0129 3.4336 2.7058 0.500E-02 0.100E-01 0.00 0.00 1.00 1.00
7.0000 5.5516 3.1475 2.6093 0.167E-02 0.333E-02 0.00 0.00 1.00 1.00
15.0000 5.8805 3.3583 2.6770 0.167E-02 0.333E-02 0.00 0.00 1.00 1.00
6.0000 7.1059 4.0081 3.0002 0.167E-02 0.333E-02 0.00 0.00 1.00 1.00
8.0000 7.1000 3.9864 3.0120 0.167E-02 0.333E-02 0.00 0.00 1.00 1.00
0.0000 7.9000 4.4036 3.2760 0.167E-02 0.333E-02 0.00 0.00 1.00 1.00
Here we tabulate the reasons for not using certain digital data sets
The following stations did not have a valid response files:
DATE=Mon May 17 13:25:48 CDT 2010