2008/03/01 07:43:15 44.22 11.19 10.0 4.8 Italy
2008/03/01 07:43:13 44.086 11.309 10 Ml:4.2 Mugello INGV
http://cnt.rm.ingv.it/~earthquake/data_id/2200726230/event.php
USGS Felt map for this earthquake
SLU Moment Tensor Solution
2008/03/01 07:43:15 44.22 11.19 10.0 4.8 Italy
Best Fitting Double Couple
Mo = 5.01e+22 dyne-cm
Mw = 4.40
Z = 8 km
Plane Strike Dip Rake
NP1 92 54 -127
NP2 325 50 -50
Principal Axes:
Axis Value Plunge Azimuth
T 5.01e+22 2 208
N 0.00e+00 29 117
P -5.01e+22 60 302
Moment Tensor: (dyne-cm)
Component Value
Mxx 3.56e+22
Mxy 2.62e+22
Mxz -1.31e+22
Myy 2.18e+21
Myz 1.73e+22
Mzz -3.78e+22
##############
######################
----------##################
---------------###############
-------------------###############
----------------------##############
-------------------------#############
------------ -------------############
------------ P --------------###########
------------- ---------------###########
--------------------------------##########
##-------------------------------#########
###------------------------------#######--
#####----------------------------####---
########-------------------------#------
#############--------------#####------
###############################-----
##############################----
############################--
### ####################--
T ###################
##############
Harvard Convention
Moment Tensor:
R T F
-3.78e+22 -1.31e+22 -1.73e+22
-1.31e+22 3.56e+22 -2.62e+22
-1.73e+22 -2.62e+22 2.18e+21
Details of the solution is found at
http://www.eas.slu.edu/Earthquake_Center/MECH.NA/20080301074315/index.html
|
STK = 325
DIP = 50
RAKE = -50
MW = 4.40
HS = 8.0
The waveform inversion is preferred.
The following compares this source inversion to others
SLU Moment Tensor Solution
2008/03/01 07:43:15 44.22 11.19 10.0 4.8 Italy
Best Fitting Double Couple
Mo = 5.01e+22 dyne-cm
Mw = 4.40
Z = 8 km
Plane Strike Dip Rake
NP1 92 54 -127
NP2 325 50 -50
Principal Axes:
Axis Value Plunge Azimuth
T 5.01e+22 2 208
N 0.00e+00 29 117
P -5.01e+22 60 302
Moment Tensor: (dyne-cm)
Component Value
Mxx 3.56e+22
Mxy 2.62e+22
Mxz -1.31e+22
Myy 2.18e+21
Myz 1.73e+22
Mzz -3.78e+22
##############
######################
----------##################
---------------###############
-------------------###############
----------------------##############
-------------------------#############
------------ -------------############
------------ P --------------###########
------------- ---------------###########
--------------------------------##########
##-------------------------------#########
###------------------------------#######--
#####----------------------------####---
########-------------------------#------
#############--------------#####------
###############################-----
##############################----
############################--
### ####################--
T ###################
##############
Harvard Convention
Moment Tensor:
R T F
-3.78e+22 -1.31e+22 -1.73e+22
-1.31e+22 3.56e+22 -2.62e+22
-1.73e+22 -2.62e+22 2.18e+21
Details of the solution is found at
http://www.eas.slu.edu/Earthquake_Center/MECH.NA/20080301074315/index.html
|
From: pondrix@bo.ingv.it
FID: AVU61
DAT: 200803010919 GMT
MW=4.73
C030108A 03/01/08 07:43:13.0 44.09 11.31 10.04.20.0NORTHERN ITALY
Nei BW: 1 1 40 SW:12 20 35 DT= 1.2 0.7 44.18 0.04 11.14 0.06 10.0 0.0
DUR 0.6 EX 23 -1.26 0.10 1.15 0.08 0.11 0.08 1.01 0.25 0.43 0.28 -0.29 0.06
1.53 19 6 0.23 16 270 -1.76 65 142 1.65 121 30 -56 263 66 -108
CENTROID, MOMENT TENSOR SOLUTION
HARVARD EVENT-FILE NAME C030108A
DATA USED: GSN
L.P. BODY WAVES: 1S, 1C, T= 40
SURFACE WAVES: 12S, 20C, T= 35
CENTROID LOCATION:
ORIGIN TIME 07:43:14.2 0.7
LAT 44.18N 0.04;LON 11.14E 0.06
DEP 10.0 FIX;HALF-DURATION 0.6
MOMENT TENSOR; SCALE 10**23 D-CM
MRR=-1.26 0.10; MTT= 1.15 0.08
MPP= 0.11 0.08; MRT= 1.01 0.25
MRP= 0.43 0.28; MTP=-0.29 0.06
PRINCIPAL AXES:
1.(T) VAL= 1.53;PLG=19;AZM= 6
2.(N) 0.23; 16; 270
3.(P) -1.76; 65; 142
BEST DOUBLE COUPLE:M0=1.6*10**23
NP1:STRIKE=121;DIP=30;SLIP= -56
NP2:STRIKE=263;DIP=66;SLIP=-108
##### ###
######### T #######
########### #########
###########################
#############################
-##############################
-############-------------#####
--######------------------------#
--##-----------------------------
-##------------------------------
####-------------- ------------
####------------- P -----------
#####------------ -----------
######-----------------------
#######-------------------#
##########----------###
###################
###########
|
INGV - DMT La soluzione graficata è ottenuta con i dati a larga banda della Rete Sismica Nazionale e della rete MedNet dell’INGV. http://cnt.rm.ingv.it/~earthquake/data_id/2200726230/map_dmt_review.jpg |
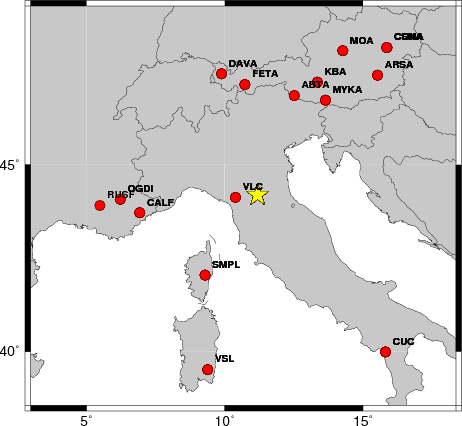
The focal mechanism was determined using broadband seismic waveforms. The location of the event and the and stations used for the waveform inversion are shown in the next figure.

|
|
|
The program wvfgrd96 was used with good traces observed at short distance to determine the focal mechanism, depth and seismic moment. This technique requires a high quality signal and well determined velocity model for the Green functions. To the extent that these are the quality data, this type of mechanism should be preferred over the radiation pattern technique which requires the separate step of defining the pressure and tension quadrants and the correct strike.
The observed and predicted traces are filtered using the following gsac commands:
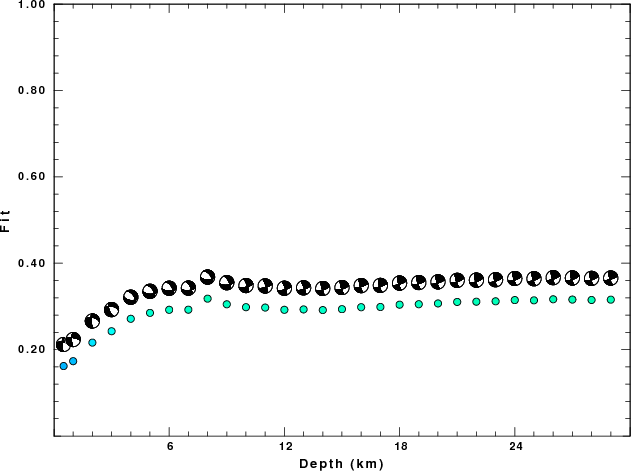
hp c 0.02 n 3 lp c 0.05 n 3The results of this grid search from 0.5 to 19 km depth are as follow:
DEPTH STK DIP RAKE MW FIT
WVFGRD96 0.5 180 70 -30 4.03 0.1620
WVFGRD96 1.0 180 70 -25 4.05 0.1733
WVFGRD96 2.0 175 75 -45 4.18 0.2163
WVFGRD96 3.0 160 60 -50 4.22 0.2426
WVFGRD96 4.0 325 50 -55 4.28 0.2714
WVFGRD96 5.0 325 50 -50 4.32 0.2851
WVFGRD96 6.0 330 55 -45 4.33 0.2922
WVFGRD96 7.0 335 60 -35 4.32 0.2925
WVFGRD96 8.0 325 50 -50 4.40 0.3180
WVFGRD96 9.0 335 60 -35 4.37 0.3049
WVFGRD96 10.0 340 75 -20 4.35 0.2983
WVFGRD96 11.0 340 80 -20 4.36 0.2974
WVFGRD96 12.0 340 80 -20 4.37 0.2922
WVFGRD96 13.0 340 85 -20 4.37 0.2931
WVFGRD96 14.0 165 80 20 4.37 0.2916
WVFGRD96 15.0 165 80 20 4.38 0.2937
WVFGRD96 16.0 165 75 15 4.39 0.2982
WVFGRD96 17.0 165 75 15 4.40 0.2987
WVFGRD96 18.0 165 75 15 4.41 0.3041
WVFGRD96 19.0 165 75 15 4.42 0.3052
WVFGRD96 20.0 165 75 15 4.42 0.3069
WVFGRD96 21.0 165 75 20 4.43 0.3104
WVFGRD96 22.0 165 75 20 4.44 0.3109
WVFGRD96 23.0 165 75 20 4.45 0.3119
WVFGRD96 24.0 165 75 20 4.45 0.3147
WVFGRD96 25.0 165 75 20 4.46 0.3141
WVFGRD96 26.0 165 75 20 4.47 0.3166
WVFGRD96 27.0 165 75 20 4.48 0.3159
WVFGRD96 28.0 165 75 20 4.48 0.3149
WVFGRD96 29.0 165 75 15 4.49 0.3157
The best solution is
WVFGRD96 8.0 325 50 -50 4.40 0.3180
The mechanism correspond to the best fit is

|
|
|
The best fit as a function of depth is given in the following figure:
|
|
|
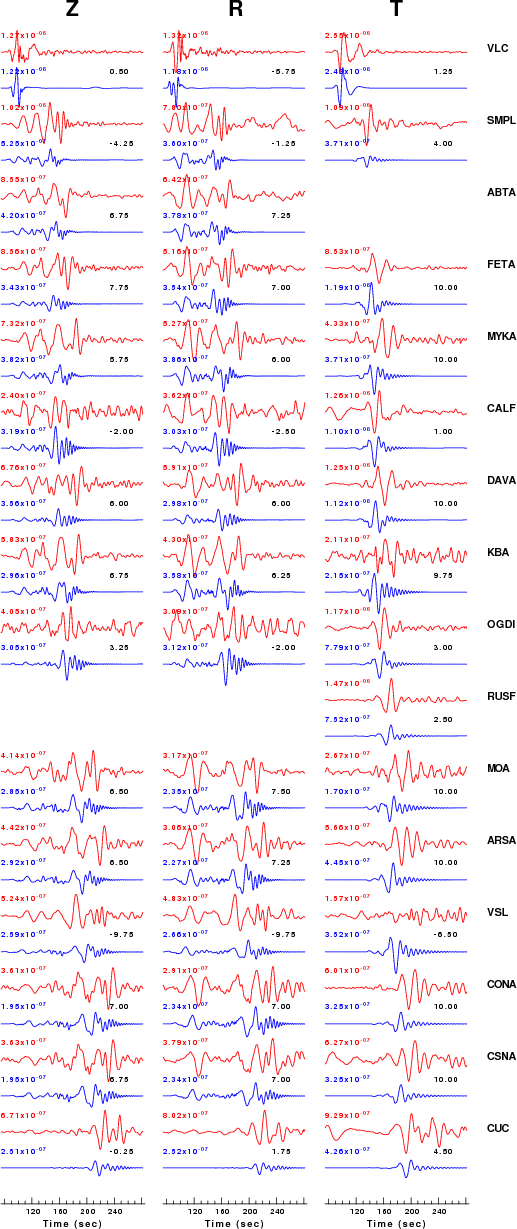
The comparison of the observed and predicted waveforms is given in the next figure. The red traces are the observed and the blue are the predicted. Each observed-predicted componnet is plotted to the same scale and peak amplitudes are indicated by the numbers to the left of each trace. The number in black at the rightr of each predicted traces it the time shift required for maximum correlation between the observed and predicted traces. This time shift is required because the synthetics are not computed at exactly the same distance as the observed and because the velocity model used in the predictions may not be perfect. A positive time shift indicates that the prediction is too fast and should be delayed to match the observed trace (shift to the right in this figure). A negative value indicates that the prediction is too slow. The bandpass filter used in the processing and for the display was
hp c 0.02 n 3 lp c 0.05 n 3
|
|
|
|
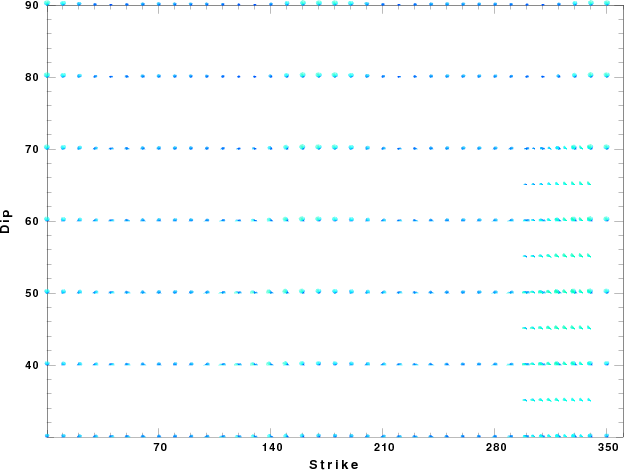
| Focal mechanism sensitivity at the preferred depth. The red color indicates a very good fit to thewavefroms. Each solution is plotted as a vector at a given value of strike and dip with the angle of the vector representing the rake angle, measured, with respect to the upward vertical (N) in the figure. |
The following figure shows the stations used in the grid search for the best focal mechanism to fit the surface-wave spectral amplitudes of the Love and Rayleigh waves.

|
|
|
The surface-wave determined focal mechanism is shown here.
 |
The P-wave first motion data for focal mechanism studies are as follow:
Sta Az(deg) Dist(km) First motion VLC 264 65 -12345 SMPL 214 282 -12345 ABTA 20 299 -12345 FETA 354 313 -12345 MYKA 35 329 -12345 CALF 263 346 -12345 DAVA 344 356 -12345 KBA 27 359 -12345 OGDI 270 397 -12345 MOA 29 468 -12345 ARSA 44 477 -12345 VSL 197 546 -12345 CONA 40 548 -12345 CSNA 40 548 -12345 CUC 139 605 -12345
Surface wave analysis was performed using codes from Computer Programs in Seismology, specifically the multiple filter analysis program do_mft and the surface-wave radiation pattern search program srfgrd96.
Digital data were collected, instrument response removed and traces converted
to Z, R an T components. Multiple filter analysis was applied to the Z and T traces to obtain the Rayleigh- and Love-wave spectral amplitudes, respectively.
These were input to the search program which examined all depths between 1 and 25 km
and all possible mechanisms.

|
|
|

|
| Pressure-tension axis trends. Since the surface-wave spectra search does not distinguish between P and T axes and since there is a 180 ambiguity in strike, all possible P and T axes are plotted. First motion data and waveforms will be used to select the preferred mechanism. The purpose of this plot is to provide an idea of the possible range of solutions. The P and T-axes for all mechanisms with goodness of fit greater than 0.9 FITMAX (above) are plotted here. |

|
| Focal mechanism sensitivity at the preferred depth. The red color indicates a very good fit to the Love and Rayleigh wave radiation patterns. Each solution is plotted as a vector at a given value of strike and dip with the angle of the vector representing the rake angle, measured, with respect to the upward vertical (N) in the figure. Because of the symmetry of the spectral amplitude rediation patterns, only strikes from 0-180 degrees are sampled. |
The distribution of broadband stations with azimuth and distance is
Sta Az(deg) Dist(km)
Since the analysis of the surface-wave radiation patterns uses only spectral amplitudes and because the surfave-wave radiation patterns have a 180 degree symmetry, each surface-wave solution consists of four possible focal mechanisms corresponding to the interchange of the P- and T-axes and a roation of the mechanism by 180 degrees. To select one mechanism, P-wave first motion can be used. This was not possible in this case because all the P-wave first motions were emergent ( a feature of the P-wave wave takeoff angle, the station location and the mechanism). The other way to select among the mechanisms is to compute forward synthetics and compare the observed and predicted waveforms.
The fits to the waveforms with the given mechanism are show below:

|
This figure shows the fit to the three components of motion (Z - vertical, R-radial and T - transverse). For each station and component, the observed traces is shown in red and the model predicted trace in blue. The traces represent filtered ground velocity in units of meters/sec (the peak value is printed adjacent to each trace; each pair of traces to plotted to the same scale to emphasize the difference in levels). Both synthetic and observed traces have been filtered using the SAC commands:

|

|
Should the national backbone of the USGS Advanced National Seismic System (ANSS) be implemented with an interstation separation of 300 km, it is very likely that an earthquake such as this would have been recorded at distances on the order of 100-200 km. This means that the closest station would have information on source depth and mechanism that was lacking here.
Dr. Harley Benz, USGS, provided the USGS USNSN digital data. The digital data used in this study were provided by Natural Resources Canada through their AUTODRM site http://www.seismo.nrcan.gc.ca/nwfa/autodrm/autodrm_req_e.php, and IRIS using their BUD interface.
Thanks also to the many seismic network operators whose dedication make this effort possible: University of Alaska, University of Washington, Oregon State University, University of Utah, Montana Bureas of Mines, UC Berkely, Caltech, UC San Diego, Saint L ouis University, Universityof Memphis, Lamont Doehrty Earth Observatory, Boston College, the Iris stations and the Transportable Array of EarthScope.
The WUS.REG used for the waveform synthetic seismograms and for the surface wave eigenfunctions and dispersion is as follows:
MODEL.01
Model after 8 iterations
ISOTROPIC
KGS
FLAT EARTH
1-D
CONSTANT VELOCITY
LINE08
LINE09
LINE10
LINE11
H(KM) VP(KM/S) VS(KM/S) RHO(GM/CC) QP QS ETAP ETAS FREFP FREFS
1.9000 3.4065 2.0089 2.2150 0.302E-02 0.679E-02 0.00 0.00 1.00 1.00
6.1000 5.5445 3.2953 2.6089 0.349E-02 0.784E-02 0.00 0.00 1.00 1.00
13.0000 6.2708 3.7396 2.7812 0.212E-02 0.476E-02 0.00 0.00 1.00 1.00
19.0000 6.4075 3.7680 2.8223 0.111E-02 0.249E-02 0.00 0.00 1.00 1.00
0.0000 7.9000 4.6200 3.2760 0.164E-10 0.370E-10 0.00 0.00 1.00 1.00
Here we tabulate the reasons for not using certain digital data sets
The following stations did not have a valid response files:
DATE=Sat Mar 1 10:14:17 CST 2008