2008/02/27 00:56:45 53.32 -0.31 10.0 4.7 England USGS
2008/02/27 00:56:43.9 53.3357 -0.4281 2.0 4.9 EMSC
USGS Felt map for this earthquake
SLU Moment Tensor Solution
2008/02/27 00:56:45 53.32 -0.31 10.0 4.7 England
Best Fitting Double Couple
Mo = 6.17e+22 dyne-cm
Mw = 4.46
Z = 25 km
Plane Strike Dip Rake
NP1 97 86 145
NP2 190 55 5
Principal Axes:
Axis Value Plunge Azimuth
T 6.17e+22 27 48
N 0.00e+00 55 271
P -6.17e+22 21 149
Moment Tensor: (dyne-cm)
Component Value
Mxx -1.74e+22
Mxy 4.81e+22
Mxz 3.44e+22
Myy 1.23e+22
Myz 7.93e+21
Mzz 5.05e+21
---------#####
----------############
------------################
-----------###################
------------############### ####
------------################ T #####
------------################# ######
-------------###########################
------------############################
-------------#############################
########----##############################
############--------######################
############------------------------------
###########-----------------------------
###########-----------------------------
##########----------------------------
#########---------------------------
#########--------------- -------
#######--------------- P -----
#######-------------- ----
#####-----------------
##------------
Harvard Convention
Moment Tensor:
R T F
5.05e+21 3.44e+22 -7.93e+21
3.44e+22 -1.74e+22 -4.81e+22
-7.93e+21 -4.81e+22 1.23e+22
Details of the solution is found at
http://www.eas.slu.edu/Earthquake_Center/MECH.NA/20080227005645/index.html
|
STK = 190
DIP = 55
RAKE = 5
MW = 4.46
HS = 25
The wavefrom inversion solution is preferred.
The following compares this source inversion to others
SLU Moment Tensor Solution
2008/02/27 00:56:45 53.32 -0.31 10.0 4.7 England
Best Fitting Double Couple
Mo = 6.17e+22 dyne-cm
Mw = 4.46
Z = 25 km
Plane Strike Dip Rake
NP1 97 86 145
NP2 190 55 5
Principal Axes:
Axis Value Plunge Azimuth
T 6.17e+22 27 48
N 0.00e+00 55 271
P -6.17e+22 21 149
Moment Tensor: (dyne-cm)
Component Value
Mxx -1.74e+22
Mxy 4.81e+22
Mxz 3.44e+22
Myy 1.23e+22
Myz 7.93e+21
Mzz 5.05e+21
---------#####
----------############
------------################
-----------###################
------------############### ####
------------################ T #####
------------################# ######
-------------###########################
------------############################
-------------#############################
########----##############################
############--------######################
############------------------------------
###########-----------------------------
###########-----------------------------
##########----------------------------
#########---------------------------
#########--------------- -------
#######--------------- P -----
#######-------------- ----
#####-----------------
##------------
Harvard Convention
Moment Tensor:
R T F
5.05e+21 3.44e+22 -7.93e+21
3.44e+22 -1.74e+22 -4.81e+22
-7.93e+21 -4.81e+22 1.23e+22
Details of the solution is found at
http://www.eas.slu.edu/Earthquake_Center/MECH.NA/20080227005645/index.html
|
EMSC Moment Tensors solutions
Provided by ETHZ, AUTH, IGN, INGV-MEDNET, KOERI, NOA_IG, HARVARD, USGS, CPPT
From: pondrix@bo.ingv.it
FID: AUX18
DAT: 200802271502 GMT
S022708A 02/27/08 00:56:43.9 53.34 -0.43 10.04.90.0UNITED KINGDOM MW=4.63
Nei BW: 0 0 0 SW:26 41 35 DT= 3.5 1.0 53.39 0.02 -0.41 0.08 25.2 1.3
DUR 0.5 EX 23 0.04 0.09 -0.41 0.06 0.37 0.05 0.38 0.07 -0.22 0.07 -0.93 0.05
1.13 20 55 -0.07 67 265 -1.06 11 149 1.10 193 68 7 100 83 158
CENTROID, MOMENT TENSOR SOLUTION
HARVARD EVENT-FILE NAME S022708A
DATA USED: GSN
SURFACE WAVES: 26S, 41C, T= 35
CENTROID LOCATION:
ORIGIN TIME 00:56:47.4 1.0
LAT 53.39N 0.02;LON 0.41W 0.08
DEP 25.2 1.3;HALF-DURATION 0.5
MOMENT TENSOR; SCALE 10**23 D-CM
MRR= 0.04 0.09; MTT=-0.41 0.06
MPP= 0.37 0.05; MRT= 0.38 0.07
MRP=-0.22 0.07; MTP=-0.93 0.05
PRINCIPAL AXES:
1.(T) VAL= 1.13;PLG=20;AZM= 55
2.(N) -0.07; 67; 265
3.(P) -1.06; 11; 149
BEST DOUBLE COUPLE:M0=1.1*10**23
NP1:STRIKE=193;DIP=68;SLIP= 7
NP2:STRIKE=100;DIP=83;SLIP= 158
---------##
-----------########
------------###########
------------########### #
-------------########### T ##
-------------############ ###
------------###################
#------------####################
######------#####################
############--###################
###########----------------######
##########---------------------
##########---------------------
#########--------------------
########------------ ----
######------------ P --
#####-----------
##---------
|
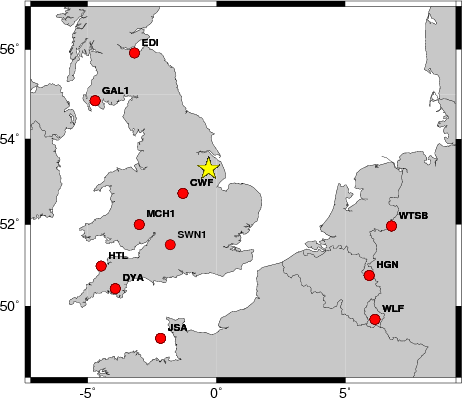
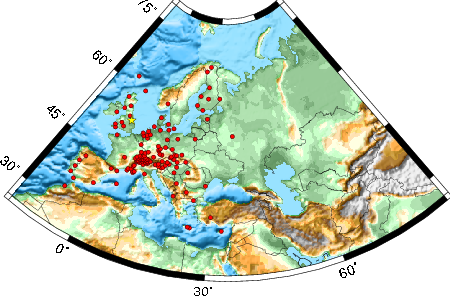
The focal mechanism was determined using broadband seismic waveforms. The location of the event and the and stations used for the waveform inversion are shown in the next figure.

|
|
|
The program wvfgrd96 was used with good traces observed at short distance to determine the focal mechanism, depth and seismic moment. This technique requires a high quality signal and well determined velocity model for the Green functions. To the extent that these are the quality data, this type of mechanism should be preferred over the radiation pattern technique which requires the separate step of defining the pressure and tension quadrants and the correct strike.
The observed and predicted traces are filtered using the following gsac commands:
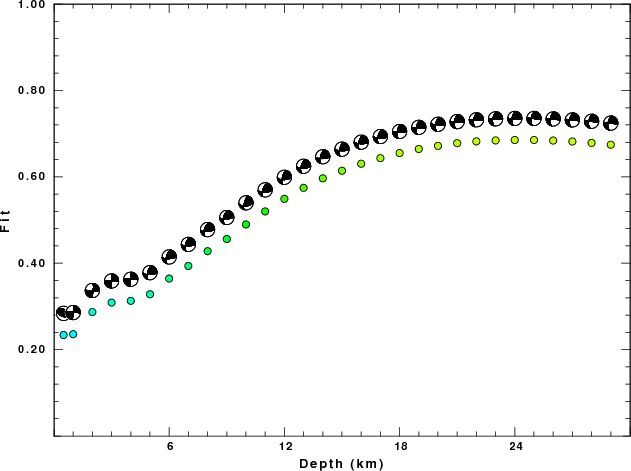
hp c 0.02 n 3 lp c 0.05 n 3The results of this grid search from 0.5 to 19 km depth are as follow:
DEPTH STK DIP RAKE MW FIT
WVFGRD96 0.5 110 50 85 3.96 0.2339
WVFGRD96 1.0 185 90 -5 4.02 0.2358
WVFGRD96 2.0 5 80 -10 4.12 0.2869
WVFGRD96 3.0 5 90 0 4.18 0.3090
WVFGRD96 4.0 185 85 -5 4.23 0.3129
WVFGRD96 5.0 195 60 30 4.30 0.3282
WVFGRD96 6.0 195 55 30 4.32 0.3646
WVFGRD96 7.0 195 55 25 4.32 0.3937
WVFGRD96 8.0 200 50 35 4.39 0.4279
WVFGRD96 9.0 195 50 25 4.39 0.4559
WVFGRD96 10.0 195 70 45 4.41 0.4898
WVFGRD96 11.0 200 60 40 4.41 0.5199
WVFGRD96 12.0 195 65 35 4.41 0.5490
WVFGRD96 13.0 195 60 30 4.41 0.5745
WVFGRD96 14.0 195 60 30 4.42 0.5965
WVFGRD96 15.0 195 60 25 4.42 0.6140
WVFGRD96 16.0 195 60 25 4.42 0.6303
WVFGRD96 17.0 195 60 25 4.43 0.6432
WVFGRD96 18.0 190 60 15 4.44 0.6550
WVFGRD96 19.0 190 60 15 4.44 0.6645
WVFGRD96 20.0 190 60 10 4.45 0.6717
WVFGRD96 21.0 190 55 10 4.45 0.6779
WVFGRD96 22.0 190 55 10 4.45 0.6820
WVFGRD96 23.0 190 55 10 4.45 0.6843
WVFGRD96 24.0 190 55 10 4.46 0.6852
WVFGRD96 25.0 190 55 5 4.46 0.6852
WVFGRD96 26.0 190 55 5 4.46 0.6840
WVFGRD96 27.0 190 55 5 4.46 0.6818
WVFGRD96 28.0 190 55 5 4.47 0.6786
WVFGRD96 29.0 190 55 5 4.47 0.6744
The best solution is
WVFGRD96 25.0 190 55 5 4.46 0.6852
The mechanism correspond to the best fit is

|
|
|
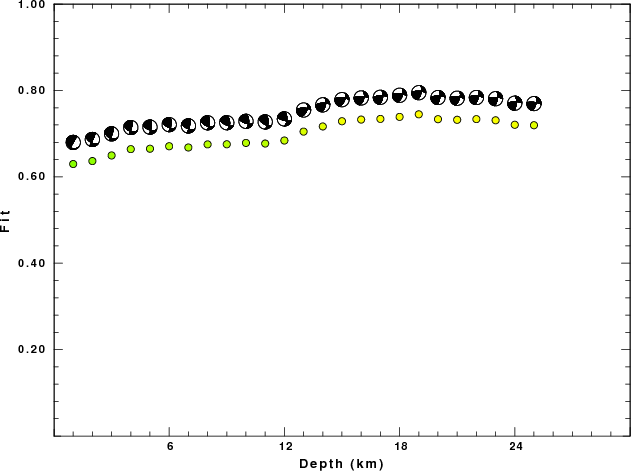
The best fit as a function of depth is given in the following figure:
|
|
|
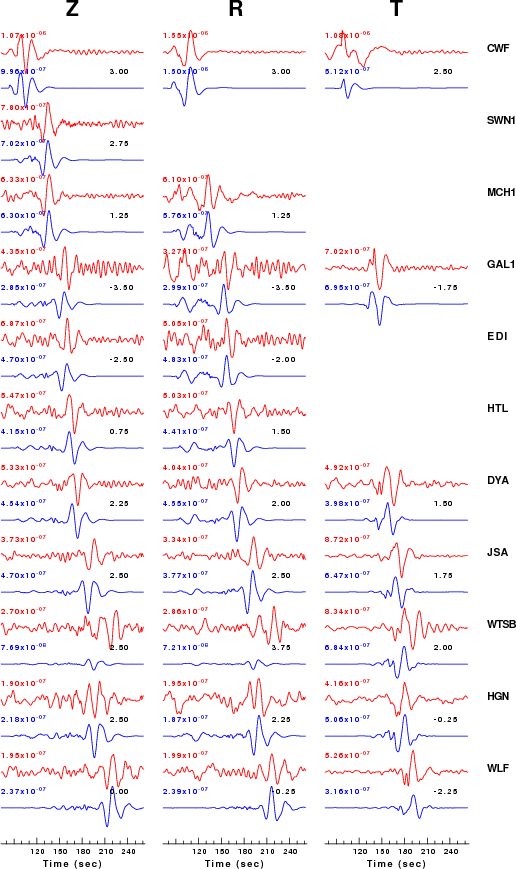
The comparison of the observed and predicted waveforms is given in the next figure. The red traces are the observed and the blue are the predicted. Each observed-predicted componnet is plotted to the same scale and peak amplitudes are indicated by the numbers to the left of each trace. The number in black at the rightr of each predicted traces it the time shift required for maximum correlation between the observed and predicted traces. This time shift is required because the synthetics are not computed at exactly the same distance as the observed and because the velocity model used in the predictions may not be perfect. A positive time shift indicates that the prediction is too fast and should be delayed to match the observed trace (shift to the right in this figure). A negative value indicates that the prediction is too slow. The bandpass filter used in the processing and for the display was
hp c 0.02 n 3 lp c 0.05 n 3
|
|
|
|
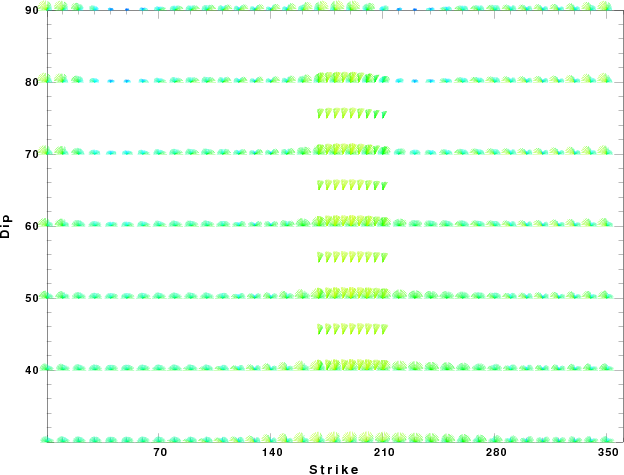
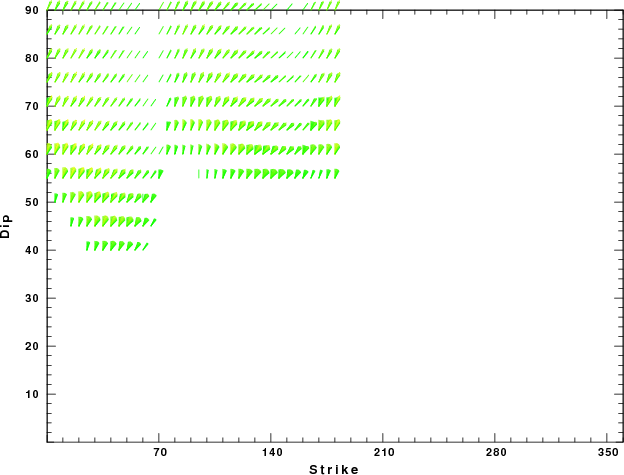
| Focal mechanism sensitivity at the preferred depth. The red color indicates a very good fit to thewavefroms. Each solution is plotted as a vector at a given value of strike and dip with the angle of the vector representing the rake angle, measured, with respect to the upward vertical (N) in the figure. |
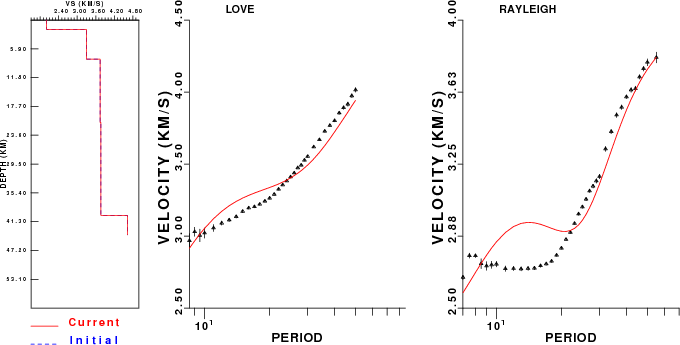
The following figure shows the stations used in the grid search for the best focal mechanism to fit the surface-wave spectral amplitudes of the Love and Rayleigh waves.
|
|
|
The surface-wave determined focal mechanism is shown here.
NODAL PLANES
STK= 91.87
DIP= 68.53
RAKE= 147.50
OR
STK= 194.99
DIP= 60.00
RAKE= 25.00
DEPTH = 19.0 km
Mw = 4.55
Best Fit 0.7447 - P-T axis plot gives solutions with FIT greater than FIT90
 |
The P-wave first motion data for focal mechanism studies are as follow:
Sta Az(deg) Dist(km) First motion CWF 226 93 -12345 HPK 310 112 -12345 SWN1 207 225 -12345 MCH1 232 234 -12345 GAL1 303 335 -12345 EDI 328 344 -12345 HTL 229 385 -12345 DSB 271 405 -12345 DYA 219 406 -12345 JSA 197 478 -12345 WTSB 105 504 -12345 HGN 121 514 -12345 WLF 130 605 -12345
Surface wave analysis was performed using codes from Computer Programs in Seismology, specifically the multiple filter analysis program do_mft and the surface-wave radiation pattern search program srfgrd96.
Digital data were collected, instrument response removed and traces converted
to Z, R an T components. Multiple filter analysis was applied to the Z and T traces to obtain the Rayleigh- and Love-wave spectral amplitudes, respectively.
These were input to the search program which examined all depths between 1 and 25 km
and all possible mechanisms.
|
|
|

|
| Pressure-tension axis trends. Since the surface-wave spectra search does not distinguish between P and T axes and since there is a 180 ambiguity in strike, all possible P and T axes are plotted. First motion data and waveforms will be used to select the preferred mechanism. The purpose of this plot is to provide an idea of the possible range of solutions. The P and T-axes for all mechanisms with goodness of fit greater than 0.9 FITMAX (above) are plotted here. |
|
| Focal mechanism sensitivity at the preferred depth. The red color indicates a very good fit to the Love and Rayleigh wave radiation patterns. Each solution is plotted as a vector at a given value of strike and dip with the angle of the vector representing the rake angle, measured, with respect to the upward vertical (N) in the figure. Because of the symmetry of the spectral amplitude rediation patterns, only strikes from 0-180 degrees are sampled. |
The distribution of broadband stations with azimuth and distance is
Sta Az(deg) Dist(km) HPK 310 112 SWN1 207 225 MCH1 232 234 GAL1 303 335 EDI 328 344 HTL 230 385 NE05 108 395 DSB 271 405 DYA 219 406 OPLO 112 458 WIT 94 471 JSA 196 478 WTSB 104 504 HLG 77 549 IBBN 98 555 BUG 109 556 KPL 325 561 WLF 130 605 MUD 56 701 BSEG 80 706 LRW 356 761 ECH 134 774 BFO 129 823 STU 123 836 BOURR 138 849 BRANT 143 859 COP 67 865 MOX 105 870 BALST 136 875 CFF 162 876 SLE 131 877 SULZ 134 878 GIMEL 145 889 TORNY 142 894 RGN 76 904 ZUR 133 914 WILA 131 927 KONO 37 930 WIMIS 139 932 MANZ 108 934 AIGLE 143 935 NKC 106 944 SENIN 142 947 HASLI 137 948 BNALP 136 950 RUE 90 951 MUO 134 952 ROTZ 110 952 EMV 144 959 LIENZ 130 966 DIX 142 978 LLS 134 980 PLONS 131 981 DAVA 129 987 FUR 120 997 FUSIO 136 998 MMK 140 1004 BSD 72 1011 BRG 100 1012 DAVOX 131 1028 WET 112 1030 VDL 134 1032 BNI 148 1050 SOFL 341 1051 FETA 127 1053 FUORN 130 1061 MUGIO 137 1063 BERNI 132 1067 OGAG 150 1072 KHC 110 1074 RUSF 156 1126 OGDI 152 1130 GKP 83 1167 KSP 97 1168 ARBF 157 1169 ABTA 124 1171 CALF 151 1189 KBA 120 1194 MOA 115 1195 ESCA 149 1196 ANTF 150 1215 CSOR 174 1222 EJON 168 1232 MYKA 121 1244 KRUC 105 1256 VRAC 104 1256 VLC 138 1284 CONA 111 1288 CSNA 111 1288 MORC 100 1296 OBKA 120 1305 ARSA 115 1311 SOKA 118 1321 OKC 100 1332 SOP 111 1346 JAVC 104 1349 ECAL 203 1353 OJC 96 1425 VYHS 104 1444 BUD 108 1514 MAHO 165 1532 MTE 204 1537 SUW 78 1547 PKSM 113 1571 RAF 48 1575 CRVS 99 1595 MEF 53 1681 PESTR 202 1700 VAF 42 1716 EMUR 183 1722 VSU 60 1772 DRGR 105 1791 DIVS 116 1802 PVAQ 201 1859 SUF 45 1861 SFS 196 1928 OUL 38 1964 TIR 104 2011 HEF 28 2096 VTS 115 2107 JOF 47 2117 RTC 196 2210 ARE0 26 2236 TIRR 104 2305 RDO 115 2358 OBN 70 2386 IDI 125 2810 LAST 125 2853 ISP 114 2920 CSS 114 3327
Since the analysis of the surface-wave radiation patterns uses only spectral amplitudes and because the surfave-wave radiation patterns have a 180 degree symmetry, each surface-wave solution consists of four possible focal mechanisms corresponding to the interchange of the P- and T-axes and a roation of the mechanism by 180 degrees. To select one mechanism, P-wave first motion can be used. This was not possible in this case because all the P-wave first motions were emergent ( a feature of the P-wave wave takeoff angle, the station location and the mechanism). The other way to select among the mechanisms is to compute forward synthetics and compare the observed and predicted waveforms.
The fits to the waveforms with the given mechanism are show below:
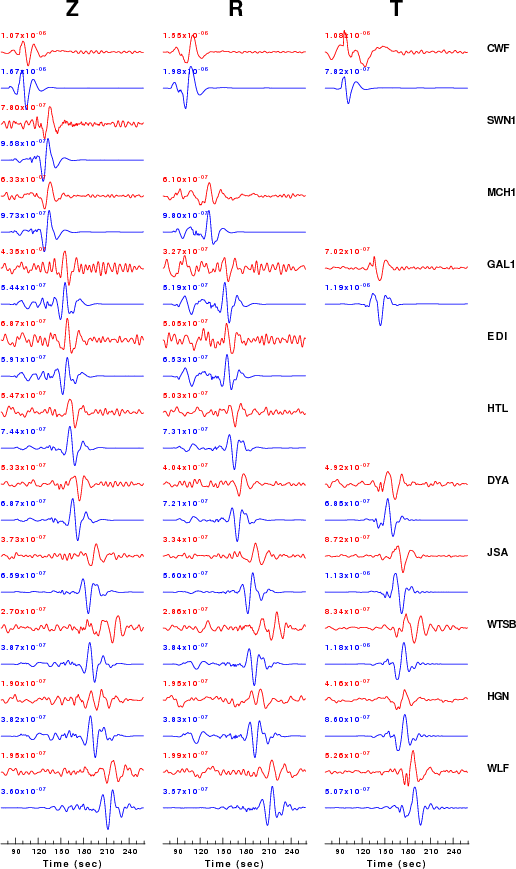
|
This figure shows the fit to the three components of motion (Z - vertical, R-radial and T - transverse). For each station and component, the observed traces is shown in red and the model predicted trace in blue. The traces represent filtered ground velocity in units of meters/sec (the peak value is printed adjacent to each trace; each pair of traces to plotted to the same scale to emphasize the difference in levels). Both synthetic and observed traces have been filtered using the SAC commands:
hp c 0.02 n 3 lp c 0.05 n 3
|
|
Should the national backbone of the USGS Advanced National Seismic System (ANSS) be implemented with an interstation separation of 300 km, it is very likely that an earthquake such as this would have been recorded at distances on the order of 100-200 km. This means that the closest station would have information on source depth and mechanism that was lacking here.
Dr. Harley Benz, USGS, provided the USGS USNSN digital data. The digital data used in this study were provided by Natural Resources Canada through their AUTODRM site http://www.seismo.nrcan.gc.ca/nwfa/autodrm/autodrm_req_e.php, and IRIS using their BUD interface.
Thanks also to the many seismic network operators whose dedication make this effort possible: University of Alaska, University of Washington, Oregon State University, University of Utah, Montana Bureas of Mines, UC Berkely, Caltech, UC San Diego, Saint L ouis University, Universityof Memphis, Lamont Doehrty Earth Observatory, Boston College, the Iris stations and the Transportable Array of EarthScope.
The VELOCITY_MODEL used for the waveform synthetic seismograms and for the surface wave eigenfunctions and dispersion is as follows:
Here we tabulate the reasons for not using certain digital data sets
The following stations did not have a valid response files:
DATE=Wed Feb 27 15:54:00 CST 2008