2006/11/17 18:19:50 43.12N 0.08E 10 4.6 France
USGS Felt map for this earthquake
USGS Felt reports page for Pyrenees, France
SLU Moment Tensor Solution
2006/11/17 18:19:50 43.12N 0.08E 10 4.6 France
Best Fitting Double Couple
Mo = 4.37e+22 dyne-cm
Mw = 4.36
Z = 12 km
Plane Strike Dip Rake
NP1 255 74 -127
NP2 145 40 -25
Principal Axes:
Axis Value Plunge Azimuth
T 4.37e+22 20 12
N 0.00e+00 36 266
P -4.37e+22 47 126
Moment Tensor: (dyne-cm)
Component Value
Mxx 2.99e+22
Mxy 1.72e+22
Mxz 2.67e+22
Myy -1.17e+22
Myz -1.48e+22
Mzz -1.82e+22
##############
############# ######
-############### T #########
--############### ##########
---###############################
----################################
----##################################
-----###################################
-----#################------------------
-------#########--------------------------
-------####-------------------------------
-------#----------------------------------
----####----------------------------------
-#######------------------- ----------
#########------------------ P ----------
##########---------------- ---------
##########--------------------------
###########-----------------------
############------------------
##############--------------
######################
##############
Harvard Convention
Moment Tensor:
R T F
-1.82e+22 2.67e+22 1.48e+22
2.67e+22 2.99e+22 -1.72e+22
1.48e+22 -1.72e+22 -1.17e+22
Details of the solution is found at
http://www.eas.slu.edu/Earthquake_Center/MECH.NA/20061117181951/index.html
|
STK = 145
DIP = 40
RAKE = -25
MW = 4.36
HS = 12
The waveform inversion is preferred. The surface-wave solution is in general agreement
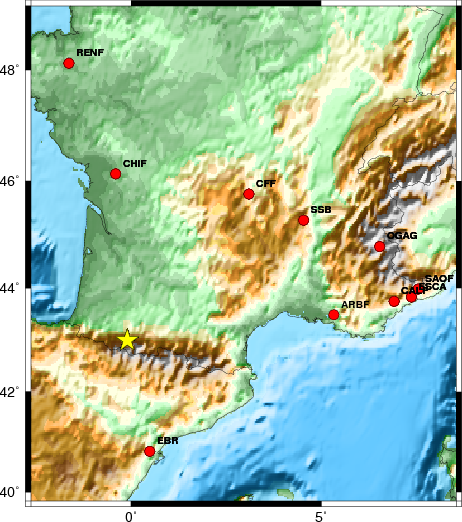
The focal mechanism was determined using broadband seismic waveforms. The location of the event and the and stations used for the waveform inversion are shown in the next figure.

|
|
|
The program wvfgrd96 was used with good traces observed at short distance to determine the focal mechanism, depth and seismic moment. This technique requires a high quality signal and well determined velocity model for the Green functions. To the extent that these are the quality data, this type of mechanism should be preferred over the radiation pattern technique which requires the separate step of defining the pressure and tension quadrants and the correct strike.
The observed and predicted traces are filtered using the following gsac commands:
hp c 0.02 n 3 lp c 0.06 n 3 br c 0.12 0.2 n 4 p 2The results of this grid search from 0.5 to 19 km depth are as follow:
DEPTH STK DIP RAKE MW FIT
WVFGRD96 0.5 200 65 30 4.14 0.4188
WVFGRD96 1.0 195 75 25 4.13 0.4048
WVFGRD96 2.0 200 75 35 4.21 0.4375
WVFGRD96 3.0 200 80 45 4.27 0.4299
WVFGRD96 4.0 150 30 -10 4.33 0.4606
WVFGRD96 5.0 145 30 -20 4.34 0.4961
WVFGRD96 6.0 145 30 -20 4.35 0.5142
WVFGRD96 7.0 140 35 -30 4.35 0.5263
WVFGRD96 8.0 140 35 -30 4.37 0.5341
WVFGRD96 9.0 140 35 -30 4.37 0.5406
WVFGRD96 10.0 145 35 -25 4.36 0.5448
WVFGRD96 11.0 145 35 -25 4.36 0.5480
WVFGRD96 12.0 145 40 -25 4.36 0.5503
WVFGRD96 13.0 145 40 -25 4.36 0.5489
WVFGRD96 14.0 150 45 -15 4.35 0.5472
WVFGRD96 15.0 160 50 20 4.36 0.5479
WVFGRD96 16.0 160 50 20 4.36 0.5451
WVFGRD96 17.0 155 55 15 4.37 0.5429
WVFGRD96 18.0 155 55 15 4.38 0.5412
WVFGRD96 19.0 155 55 15 4.38 0.5359
WVFGRD96 20.0 155 60 20 4.39 0.5323
WVFGRD96 21.0 160 50 20 4.42 0.5236
WVFGRD96 22.0 160 50 20 4.43 0.5175
WVFGRD96 23.0 160 50 20 4.43 0.5116
WVFGRD96 24.0 160 55 20 4.44 0.5035
WVFGRD96 25.0 160 55 20 4.44 0.4965
WVFGRD96 26.0 160 55 20 4.45 0.4892
WVFGRD96 27.0 160 55 20 4.46 0.4801
WVFGRD96 28.0 160 55 20 4.46 0.4714
WVFGRD96 29.0 160 55 20 4.47 0.4622
The best solution is
WVFGRD96 12.0 145 40 -25 4.36 0.5503
The mechanism correspond to the best fit is
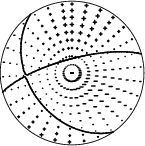
|
|
|
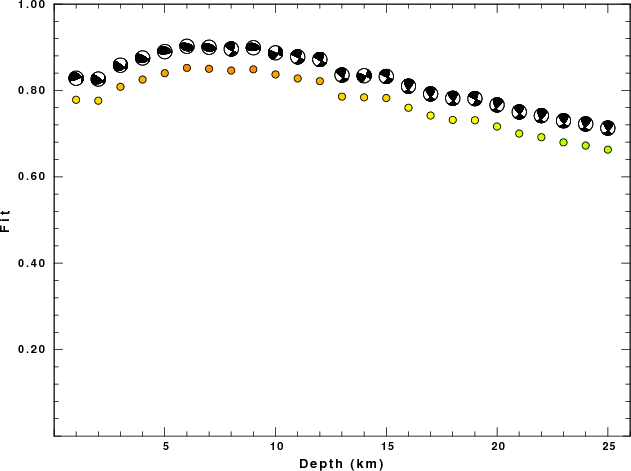
The best fit as a function of depth is given in the following figure:
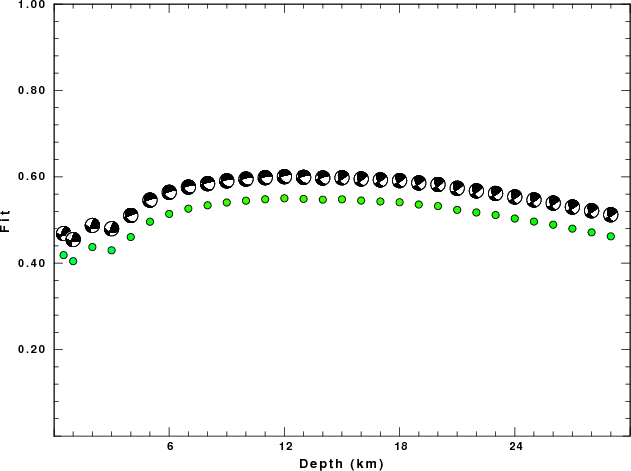
|
|
|
The comparison of the observed and predicted waveforms is given in the next figure. The red traces are the observed and the blue are the predicted. Each observed-predicted componnet is plotted to the same scale and peak amplitudes are indicated by the numbers to the left of each trace. The number in black at the rightr of each predicted traces it the time shift required for maximum correlation between the observed and predicted traces. This time shift is required because the synthetics are not computed at exactly the same distance as the observed and because the velocity model used in the predictions may not be perfect. A positive time shift indicates that the prediction is too fast and should be delayed to match the observed trace (shift to the right in this figure). A negative value indicates that the prediction is too slow. The bandpass filter used in the processing and for the display was
hp c 0.02 n 3 lp c 0.06 n 3 br c 0.12 0.2 n 4 p 2
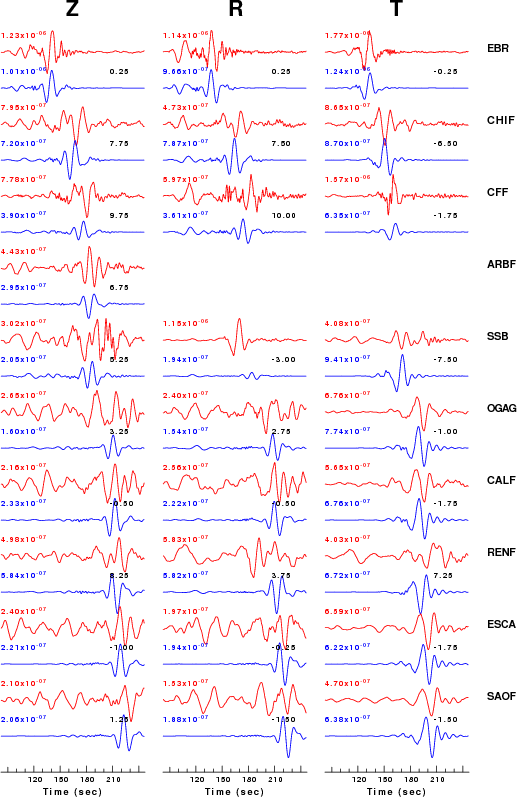
|
|
|
|
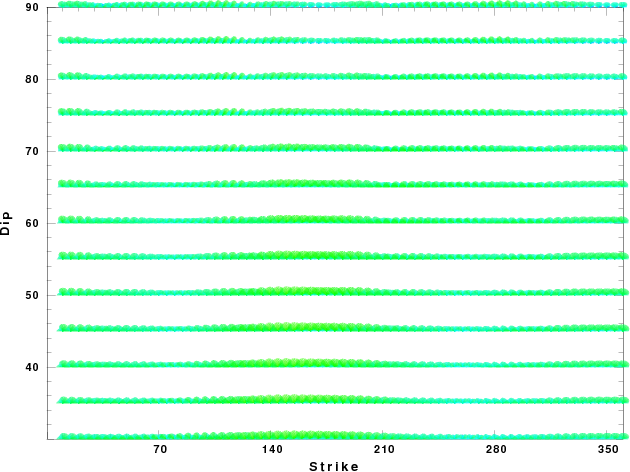
| Focal mechanism sensitivity at the preferred depth. The red color indicates a very good fit to thewavefroms. Each solution is plotted as a vector at a given value of strike and dip with the angle of the vector representing the rake angle, measured, with respect to the upward vertical (N) in the figure. |
The following figure shows the stations used in the grid search for the best focal mechanism to fit the surface-wave spectral amplitudes of the Love and Rayleigh waves.
|
|
|
The surface-wave determined focal mechanism is shown here.
NODAL PLANES
STK= 284.99
DIP= 55.00
RAKE= -90.01
OR
STK= 105.00
DIP= 35.00
RAKE= -89.99
DEPTH = 6.0 km
Mw = 4.48
Best Fit 0.8522 - P-T axis plot gives solutions with FIT greater than FIT90
 |
The P-wave first motion data for focal mechanism studies are as follow:
Sta Az(deg) Dist(km) First motion EBR 168 247 eP_+ CHIF 356 349 iP_D CFF 39 399 eP_X ARBF 81 445 eP_X SSB 54 450 eP_X OGAG 67 569 eP_X CALF 79 575 eP_X RENF 349 582 eP_X ESCA 79 612 eP_X SAOF 77 629 eP_X
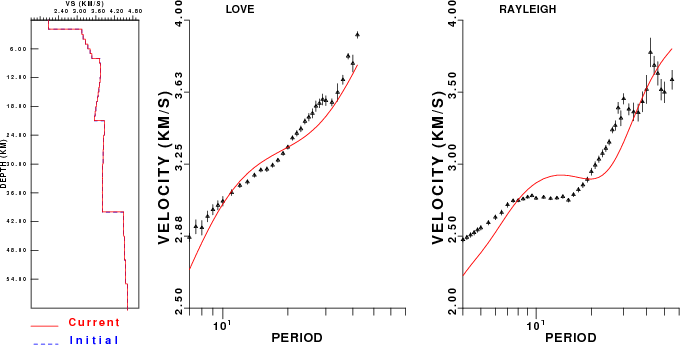
Surface wave analysis was performed using codes from Computer Programs in Seismology, specifically the multiple filter analysis program do_mft and the surface-wave radiation pattern search program srfgrd96.
The velocity model used for the search is a modified Utah model .
Digital data were collected, instrument response removed and traces converted
to Z, R an T components. Multiple filter analysis was applied to the Z and T traces to obtain the Rayleigh- and Love-wave spectral amplitudes, respectively.
These were input to the search program which examined all depths between 1 and 25 km
and all possible mechanisms.
|
|
|

|
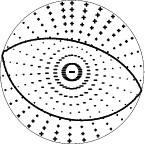
| Pressure-tension axis trends. Since the surface-wave spectra search does not distinguish between P and T axes and since there is a 180 ambiguity in strike, all possible P and T axes are plotted. First motion data and waveforms will be used to select the preferred mechanism. The purpose of this plot is to provide an idea of the possible range of solutions. The P and T-axes for all mechanisms with goodness of fit greater than 0.9 FITMAX (above) are plotted here. |
|
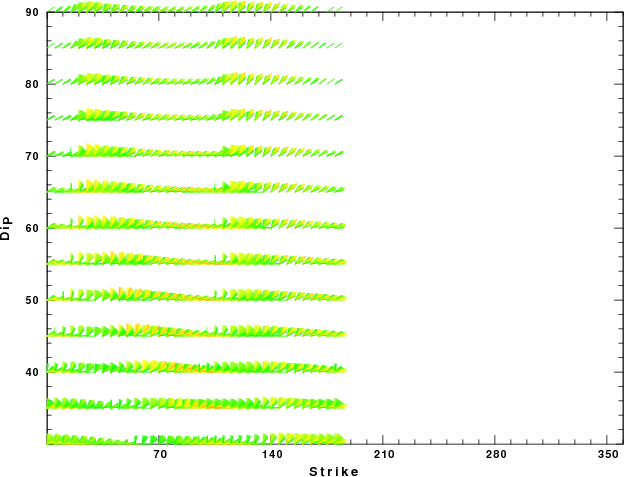
| Focal mechanism sensitivity at the preferred depth. The red color indicates a very good fit to the Love and Rayleigh wave radiation patterns. Each solution is plotted as a vector at a given value of strike and dip with the angle of the vector representing the rake angle, measured, with respect to the upward vertical (N) in the figure. Because of the symmetry of the spectral amplitude rediation patterns, only strikes from 0-180 degrees are sampled. |
Sta Az(deg) Dist(km) EBR 168 247 CHIF 356 349 CFF 39 399 SSB 54 450 OGDI 74 526 OGAG 67 569 CALF 79 575 RENF 349 582 BNI 65 589 ANTI 81 590 ESCA 79 612 SAOF 77 629 SENIN 55 695 BOURR 47 755 BNALP 54 799 WLF 31 883 SFS 218 894 PMST 241 900 DAVA 55 918 WOL 355 928 HTL 341 949 HGN 26 978
Since the analysis of the surface-wave radiation patterns uses only spectral amplitudes and because the surfave-wave radiation patterns have a 180 degree symmetry, each surface-wave solution consists of four possible focal mechanisms corresponding to the interchange of the P- and T-axes and a roation of the mechanism by 180 degrees. To select one mechanism, P-wave first motion can be used. This was not possible in this case because all the P-wave first motions were emergent ( a feature of the P-wave wave takeoff angle, the station location and the mechanism). The other way to select among the mechanisms is to compute forward synthetics and compare the observed and predicted waveforms.
The velocity model used for the waveform fit is a modified Utah model .
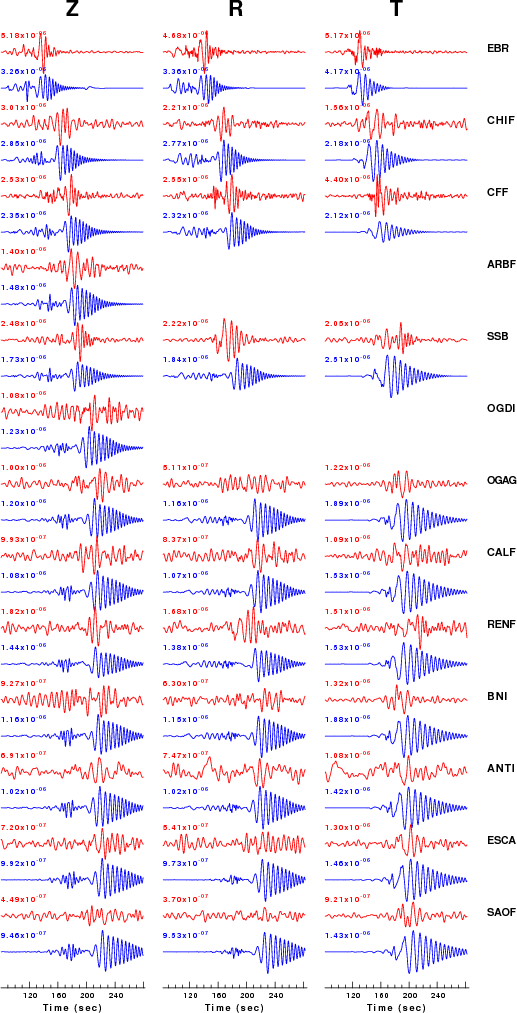
The fits to the waveforms with the given mechanism are show below:
|
This figure shows the fit to the three components of motion (Z - vertical, R-radial and T - transverse). For each station and component, the observed traces is shown in red and the model predicted trace in blue. The traces represent filtered ground velocity in units of meters/sec (the peak value is printed adjacent to each trace; each pair of traces to plotted to the same scale to emphasize the difference in levels). Both synthetic and observed traces have been filtered using the SAC commands:
hp c 0.02 n 3 lp c 0.10 n 3
|
|
Should the national backbone of the USGS Advanced National Seismic System (ANSS) be implemented with an interstation separation of 300 km, it is very likely that an earthquake such as this would have been recorded at distances on the order of 100-200 km. This means that the closest station would have information on source depth and mechanism that was lacking here.
Dr. Harley Benz, USGS, provided the USGS USNSN digital data. The digital data used in this study were provided by Natural Resources Canada through their AUTODRM site http://www.seismo.nrcan.gc.ca/nwfa/autodrm/autodrm_req_e.php, and IRIS using their BUD interface
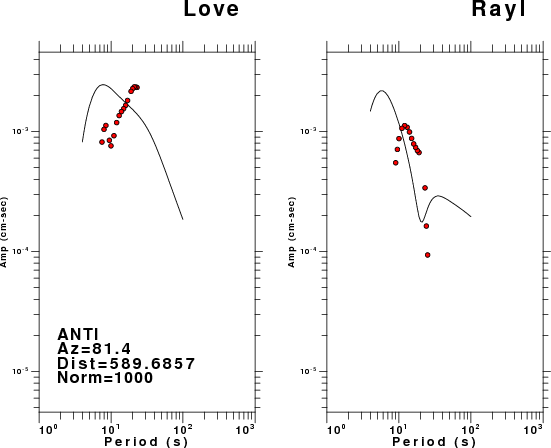
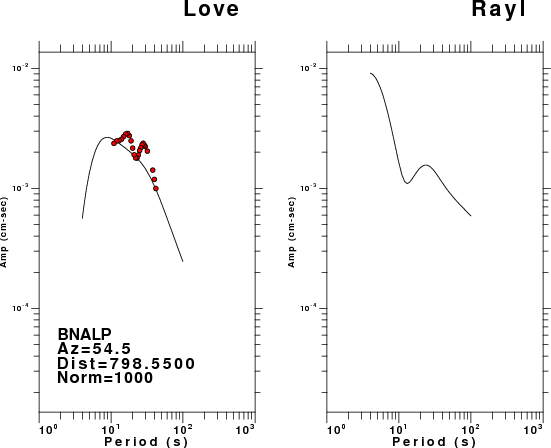
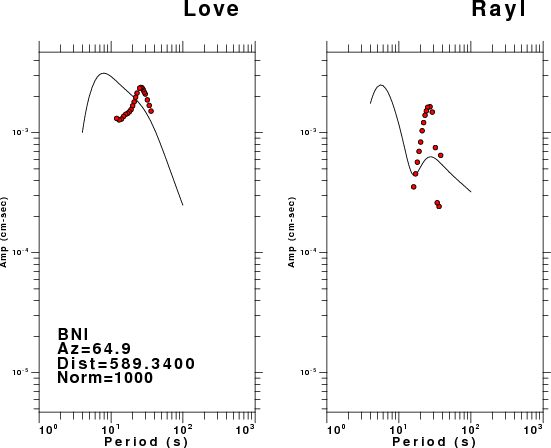
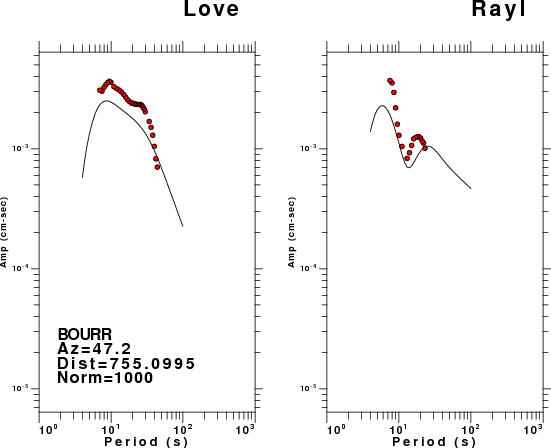
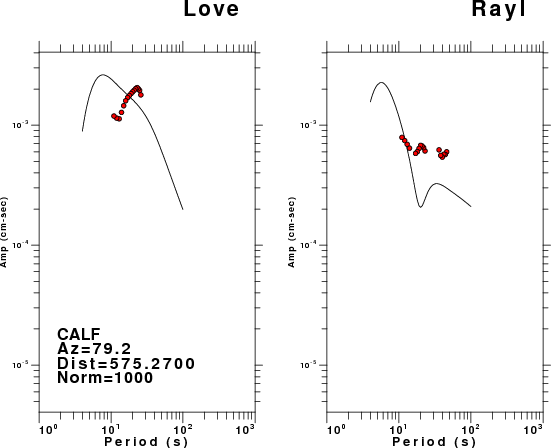
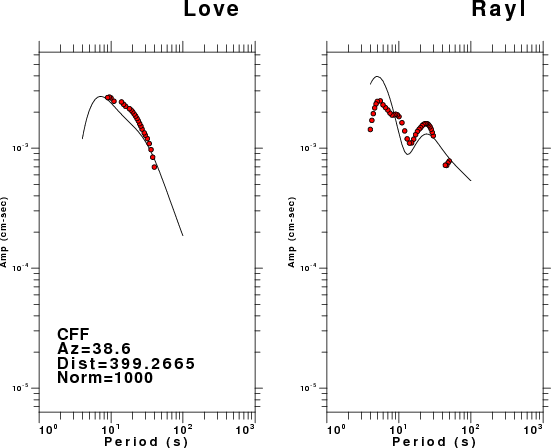
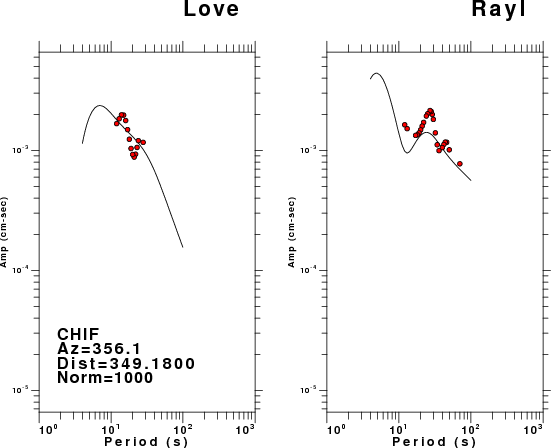
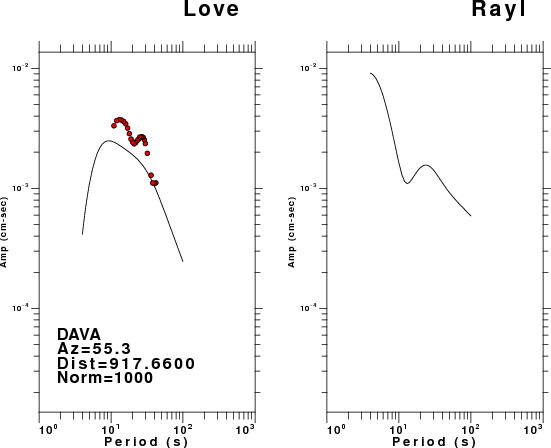
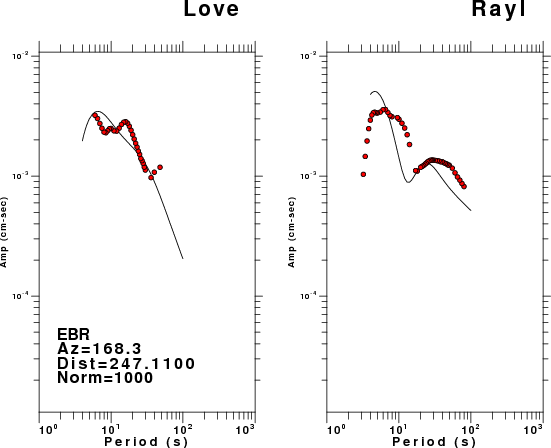
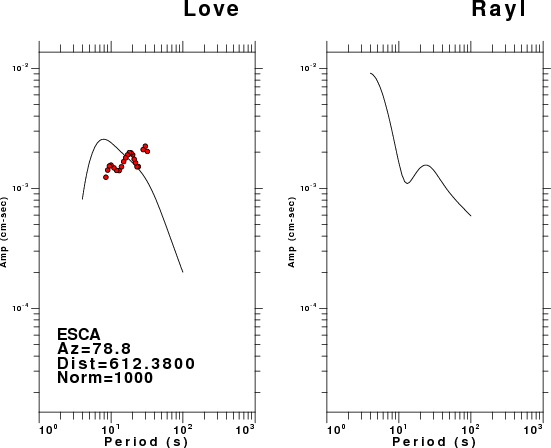
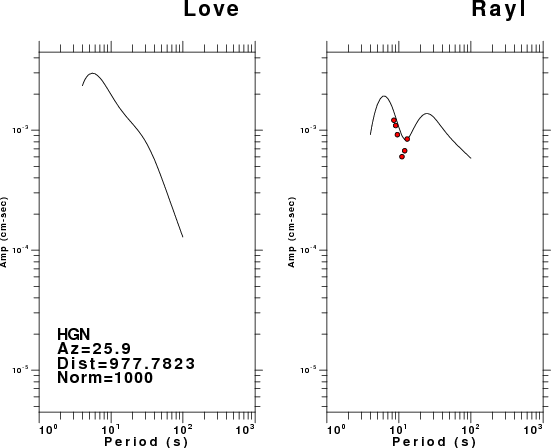
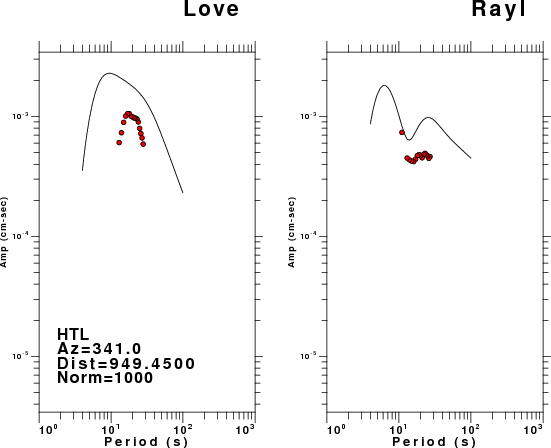
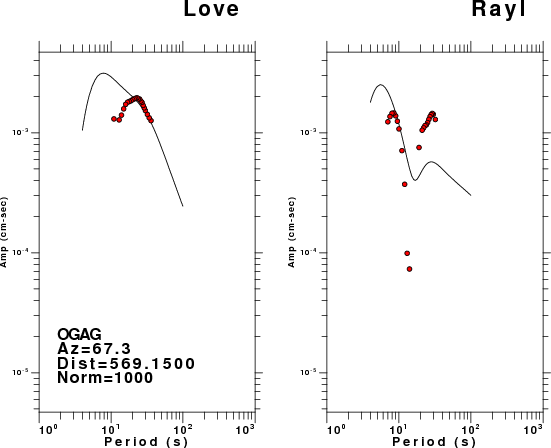
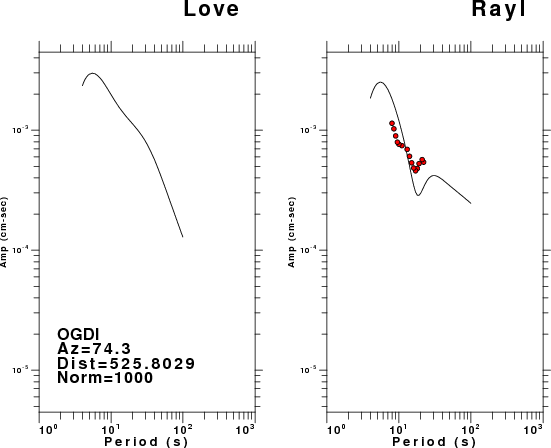
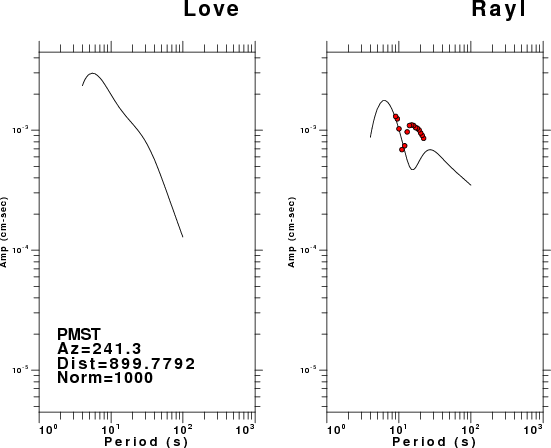
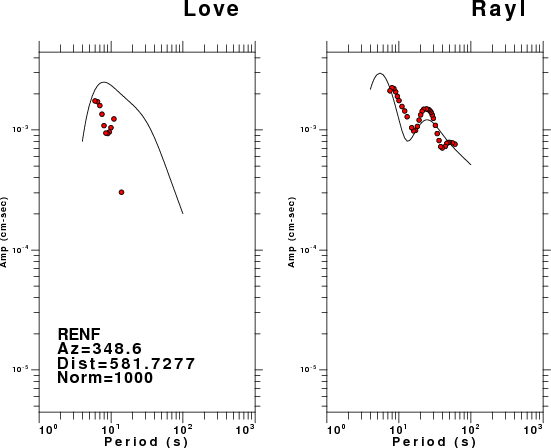
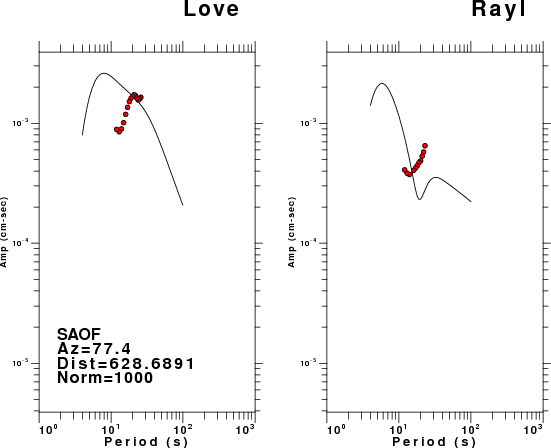
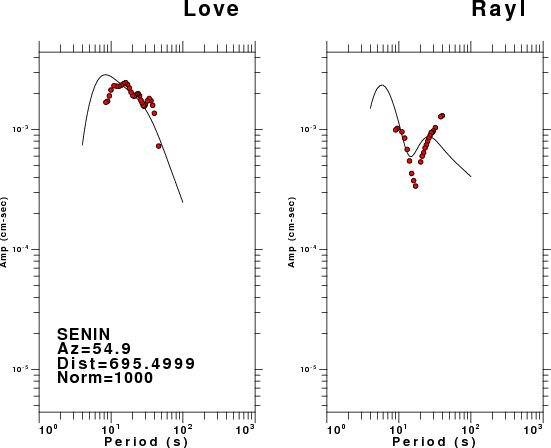
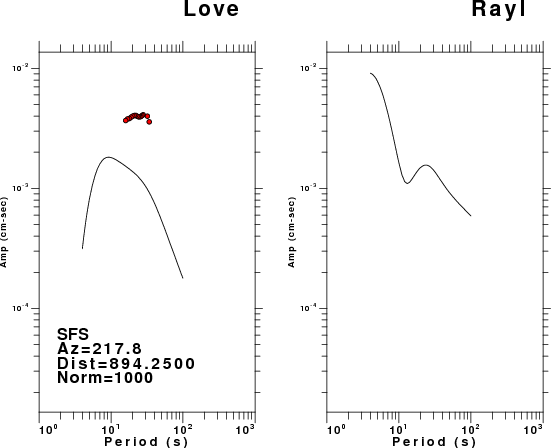
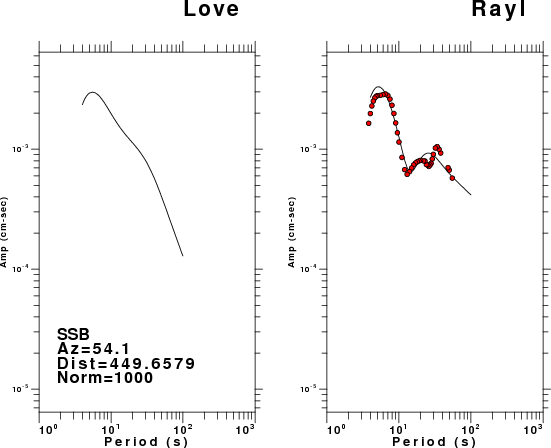
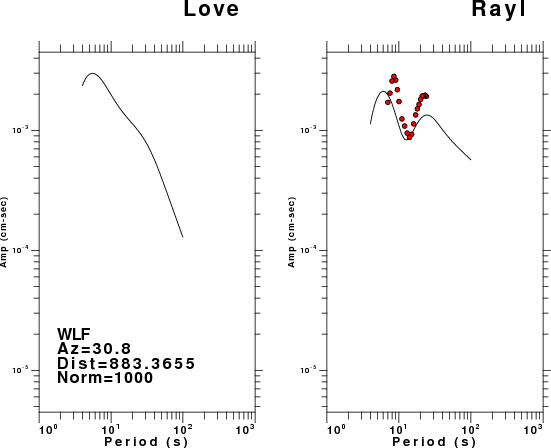
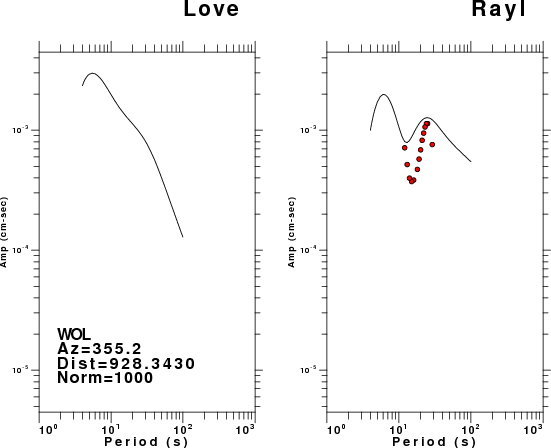
The figures below show the observed spectral amplitudes (units of cm-sec) at each station and the
theoretical predictions as a function of period for the mechanism given above. The modified Utah model earth model
was used to define the Green's functions. For each station, the Love and Rayleigh wave spectrail amplitudes are plotted with the same scaling so that one can get a sense fo the effects of the effects of the focal mechanism and depth on the excitation of each.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Here we tabulate the reasons for not using certain digital data sets
The following stations did not have a valid response files: