2004/02/24 05:21:26 15.43N 40.72E 10 4.0 Italy
USGS Felt map for this earthquake
SLU Moment Tensor Solution
2004/02/24 05:21:26 15.43N 40.72E 10 4.0 Italy
Best Fitting Double Couple
Mo = 1.50e+22 dyne-cm
Mw = 4.05
Z = 12 km
Plane Strike Dip Rake
NP1 288 68 -125
NP2 170 40 -35
Principal Axes:
Axis Value Plunge Azimuth
T 1.50e+22 16 43
N 0.00e+00 32 302
P -1.50e+22 53 156
Moment Tensor: (dyne-cm)
Component Value
Mxx 2.95e+21
Mxy 8.85e+21
Mxz 9.51e+21
Myy 5.50e+21
Myz -1.63e+20
Mzz -8.45e+21
--############
----##################
-----#######################
-----##################### #
------###################### T ###
-------###################### ####
-------###############################
########---------#######################
#######----------------#################
########---------------------#############
########------------------------##########
#########--------------------------#######
#########----------------------------#####
########------------------------------##
#########------------- ---------------
#########------------ P --------------
#########----------- -------------
#########-------------------------
########----------------------
#########-------------------
########--------------
#######-------
Harvard Convention
Moment Tensor:
R T F
-8.45e+21 9.51e+21 1.63e+20
9.51e+21 2.95e+21 -8.85e+21
1.63e+20 -8.85e+21 5.50e+21
Details of the solution is found at
http://www.eas.slu.edu/Earthquake_Center/MECH.NA/20040224052126/index.html
|
STK = 170
DIP = 40
RAKE = -35
MW = 4.05
HS = 12
The focal mechanism was determined using broadband seismic waveforms. The location of the event and the and stations used for the waveform inversion are shown in the next figure.

|
|
|
The program wvfgrd96 was used with good traces observed at short distance to determine the focal mechanism, depth and seismic moment. This technique requires a high quality signal and well determined velocity model for the Green functions. To the extent that these are the quality data, this type of mechanism should be preferred over the radiation pattern technique which requires the separate step of defining the pressure and tension quadrants and the correct strike.
The observed and predicted traces are filtered using the following gsac commands:
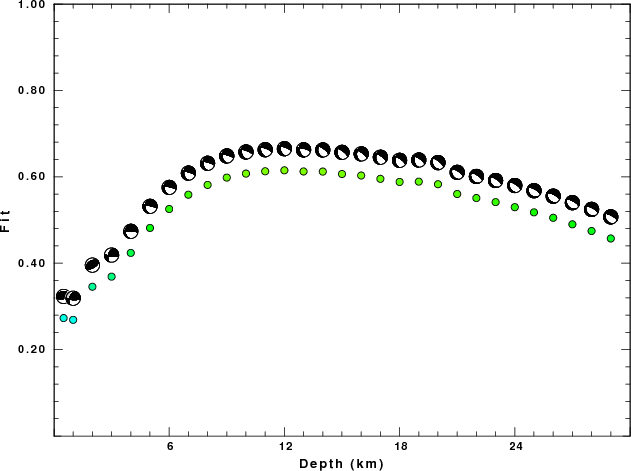
hp c 0.02 n 3 lp c 0.10 n 3The results of this grid search from 0.5 to 19 km depth are as follow:
DEPTH STK DIP RAKE MW FIT
WVFGRD96 0.5 270 30 100 3.67 0.2731
WVFGRD96 1.0 205 45 30 3.64 0.2690
WVFGRD96 2.0 60 55 90 3.80 0.3456
WVFGRD96 3.0 200 50 20 3.81 0.3689
WVFGRD96 4.0 185 25 0 3.87 0.4239
WVFGRD96 5.0 180 30 -15 3.90 0.4817
WVFGRD96 6.0 180 30 -15 3.92 0.5255
WVFGRD96 7.0 175 35 -25 3.95 0.5586
WVFGRD96 8.0 175 35 -25 3.99 0.5813
WVFGRD96 9.0 175 35 -25 4.01 0.5983
WVFGRD96 10.0 170 35 -35 4.03 0.6075
WVFGRD96 11.0 170 35 -35 4.04 0.6128
WVFGRD96 12.0 170 40 -35 4.05 0.6151
WVFGRD96 13.0 170 40 -30 4.06 0.6124
WVFGRD96 14.0 175 30 -45 4.11 0.6122
WVFGRD96 15.0 175 30 -45 4.11 0.6066
WVFGRD96 16.0 185 35 -35 4.12 0.6031
WVFGRD96 17.0 185 35 -35 4.13 0.5954
WVFGRD96 18.0 180 35 -40 4.14 0.5882
WVFGRD96 19.0 180 35 -40 4.14 0.5889
WVFGRD96 20.0 155 25 -65 4.16 0.5829
WVFGRD96 21.0 160 25 -55 4.21 0.5603
WVFGRD96 22.0 155 25 -60 4.22 0.5509
WVFGRD96 23.0 155 25 -60 4.23 0.5414
WVFGRD96 24.0 160 25 -55 4.24 0.5298
WVFGRD96 25.0 140 25 -70 4.24 0.5178
WVFGRD96 26.0 145 25 -65 4.25 0.5052
WVFGRD96 27.0 140 25 -70 4.25 0.4901
WVFGRD96 28.0 150 25 -60 4.26 0.4746
WVFGRD96 29.0 155 25 -55 4.26 0.4573
The best solution is
WVFGRD96 12.0 170 40 -35 4.05 0.6151
The mechanism correspond to the best fit is
|
|
|
|
The best fit as a function of depth is given in the following figure:
|
|
|
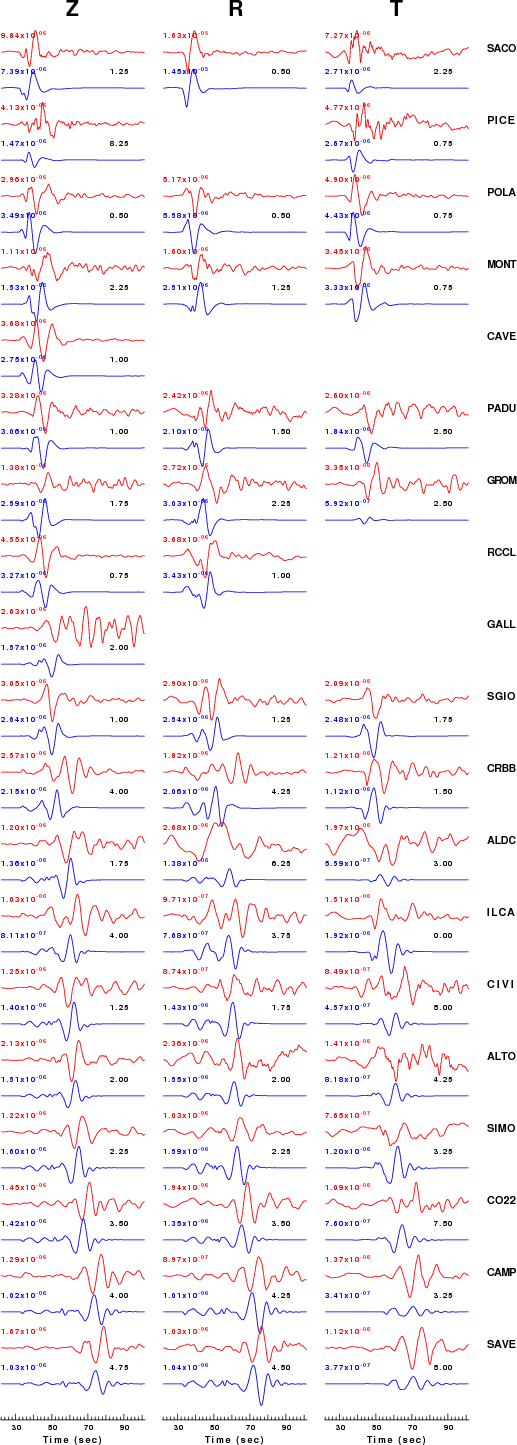
The comparison of the observed and predicted waveforms is given in the next figure. The red traces are the observed and the blue are the predicted. Each observed-predicted componnet is plotted to the same scale and peak amplitudes are indicated by the numbers to the left of each trace. The number in black at the rightr of each predicted traces it the time shift required for maximum correlation between the observed and predicted traces. This time shift is required because the synthetics are not computed at exactly the same distance as the observed and because the velocity model used in the predictions may not be perfect. A positive time shift indicates that the prediction is too fast and should be delayed to match the observed trace (shift to the right in this figure). A negative value indicates that the prediction is too slow. The bandpass filter used in the processing and for the display was
hp c 0.02 n 3 lp c 0.10 n 3
|
|
|
|
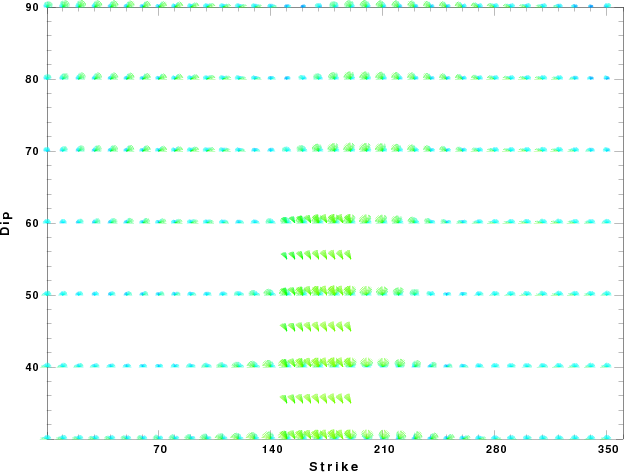
| Focal mechanism sensitivity at the preferred depth. The red color indicates a very good fit to thewavefroms. Each solution is plotted as a vector at a given value of strike and dip with the angle of the vector representing the rake angle, measured, with respect to the upward vertical (N) in the figure. |
The following figure shows the stations used in the grid search for the best focal mechanism to fit the surface-wave spectral amplitudes of the Love and Rayleigh waves.

|
|
|
The surface-wave determined focal mechanism is shown here.
 |
The P-wave first motion data for focal mechanism studies are as follow:
Sta Az(deg) Dist(km) First motion SACO 338 15 iP_D PICE 117 22 eP_+ POLA 169 24 iP_C SX17 87 35 iP_C MONT 290 38 eP_+ PIAG 187 42 iP_C VENO 50 43 iP_C CAVE 227 44 iP_C PADU 155 47 eP_- GROM 321 50 eP_- RCCL 215 57 iP_C TRIC 101 58 eP_+ GALL 128 75 eP_X SGIO 179 75 eP_+ CRBB 60 81 eP_+ CRAC 114 93 eP_X ALDC 136 117 eP_X ILCA 95 122 iP_C CIVI 143 124 eP_X ALTO 153 129 eP_X SIMO 162 141 eP_X CO22 151 155 eP_X CAMP 140 188 eP_+ SAVE 143 194 eP_+
Surface wave analysis was performed using codes from Computer Programs in Seismology, specifically the multiple filter analysis program do_mft and the surface-wave radiation pattern search program srfgrd96.
The velocity model used for the search is a modified Utah model .
Digital data were collected, instrument response removed and traces converted
to Z, R an T components. Multiple filter analysis was applied to the Z and T traces to obtain the Rayleigh- and Love-wave spectral amplitudes, respectively.
These were input to the search program which examined all depths between 1 and 25 km
and all possible mechanisms.

|
|
|

|
| Pressure-tension axis trends. Since the surface-wave spectra search does not distinguish between P and T axes and since there is a 180 ambiguity in strike, all possible P and T axes are plotted. First motion data and waveforms will be used to select the preferred mechanism. The purpose of this plot is to provide an idea of the possible range of solutions. The P and T-axes for all mechanisms with goodness of fit greater than 0.9 FITMAX (above) are plotted here. |

|
| Focal mechanism sensitivity at the preferred depth. The red color indicates a very good fit to the Love and Rayleigh wave radiation patterns. Each solution is plotted as a vector at a given value of strike and dip with the angle of the vector representing the rake angle, measured, with respect to the upward vertical (N) in the figure. Because of the symmetry of the spectral amplitude rediation patterns, only strikes from 0-180 degrees are sampled. |
Sta Az(deg) Dist(km)
Since the analysis of the surface-wave radiation patterns uses only spectral amplitudes and because the surfave-wave radiation patterns have a 180 degree symmetry, each surface-wave solution consists of four possible focal mechanisms corresponding to the interchange of the P- and T-axes and a roation of the mechanism by 180 degrees. To select one mechanism, P-wave first motion can be used. This was not possible in this case because all the P-wave first motions were emergent ( a feature of the P-wave wave takeoff angle, the station location and the mechanism). The other way to select among the mechanisms is to compute forward synthetics and compare the observed and predicted waveforms.
The velocity model used for the waveform fit is a modified Utah model .
The fits to the waveforms with the given mechanism are show below:

|
This figure shows the fit to the three components of motion (Z - vertical, R-radial and T - transverse). For each station and component, the observed traces is shown in red and the model predicted trace in blue. The traces represent filtered ground velocity in units of meters/sec (the peak value is printed adjacent to each trace; each pair of traces to plotted to the same scale to emphasize the difference in levels). Both synthetic and observed traces have been filtered using the SAC commands:

|

|
Should the national backbone of the USGS Advanced National Seismic System (ANSS) be implemented with an interstation separation of 300 km, it is very likely that an earthquake such as this would have been recorded at distances on the order of 100-200 km. This means that the closest station would have information on source depth and mechanism that was lacking here.
Dr. Harley Benz, USGS, provided the USGS USNSN digital data. The digital data used in this study were provided by Natural Resources Canada through their AUTODRM site http://www.seismo.nrcan.gc.ca/nwfa/autodrm/autodrm_req_e.php, and IRIS using their BUD interface
The figures below show the observed spectral amplitudes (units of cm-sec) at each station and the
theoretical predictions as a function of period for the mechanism given above. The modified Utah model earth model
was used to define the Green's functions. For each station, the Love and Rayleigh wave spectrail amplitudes are plotted with the same scaling so that one can get a sense fo the effects of the effects of the focal mechanism and depth on the excitation of each.
Here we tabulate the reasons for not using certain digital data sets
The following stations did not have a valid response files: